1.1 Probabilità

3. Teoremi sul calcolo della probabilità

3.1. Esempio di applicazione dei teoremi

PRIMO ESEMPIO

Un’urna contiene 20 palline, di cui 12 bianche e 8 nere.

Si estraggono due palline, senza reinserire nell’urna la prima estratta.

Qual è la probabilità che siano dello stesso colore?

Si tratta di calcolare la probabilità dell’unione di due eventi incompatibili:

$E_1$ “le due palline estratte sono entrambe bianche”

$E_2$ “le due palline estratte sono entrambe nere”

Partiamo dall’evento $E_1$ “le due palline estratte sono entrambe bianche”. Questo significa che la prima pallina estratta è bianca e che la seconda pallina estratta è bianca. Notiamo la congiunzione “e” che ci suggerisce una intersezione tra i due eventi:

$E_{11}$ “la prima pallina estratta è bianca”

$E_{12}$ “la seconda pallina estratta è bianca”

Nel nostro caso i due eventi sono dipendenti in quanto l’estrazione della seconda pallina dipende dalla prima estratta e non reinserita nell’urna e quindi vale:

$p(E_{11} ∩ E_{12}) = p(E_{11}) · p(E_{12}|E_{11}) = \dfrac{12}{20} · \dfrac{11}{19} = 0,35 = 35 \%$

$p(E_{11})$ e $p(E_{12}|E_{11})$ sono stati calcolati come rapporto tra il numero di esiti favorevoli e il numero di esiti possibili:

per $E_{11}$ si hanno $12$ esiti favorevoli e $20$ possibili quindi $p(E_{11}) = \dfrac{12}{20}$

per $E_{12}|E_{11}$ si hanno $11$ esiti favorevoli e $19$ possibili quindi $p(E_{12}|E_{11}) = \dfrac{11}{19}$

Passiamo all’evento $E_2$ “le due palline estratte sono entrambe nere”. Si applica lo stesso ragionamento trovando:

$p(E_2) = 0,15 = 15 \%$

Lasciamo al lettore la possibilità di sviluppare i passaggi nel dettaglio.

Per rispondere alla domanda iniziale, si calcola la probabilità dell’unione dei due eventi $E_1$ ed $E_2$ che abbiamo detto essere incompatibili:

$p(E_1 \cup E_2) = p(E_1) + p(E_2) = 0,35 + 0,15 = 0,50 = 50 \%$

In conclusione la probabilità che le due palline estratte dall’urna siano dello stesso colore è del $50 \%$ .

SECONDO ESEMPIO

Determinare la probabilità matematica che una coppia abbia tre figlie femmine

Utilizziamo, ad esempio, un diagramma ad albero per rappresentare i casi possibili in modo da avere un'elencazione grafica di tutti gli elementi dello spazio campione (indichiamo con 1F= primo figlio, 2F=secondo figlio, 3F=terzo figlio).

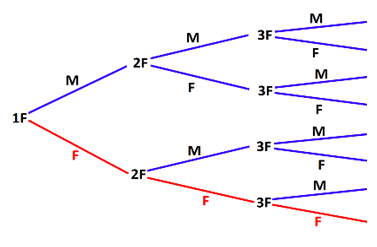
Se scriviamo su ciascun ramo la probabilità dell'evento rappresentato nel nodo seguente, avremo che la probabilità di uno qualsiasi degli eventi sui rami terminali è data dal prodotto delle probabilità scritte sull'intero percorso (questa regola è detta regola del prodotto).
Poichè la probabilità che nasca un figlio maschio o che nasca un figlio femmina è in entrambi i casi uguale a $\dfrac{1}{2}$ , avremo che:

$p(3F) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2}=\dfrac{1}{8}$