1.1 Definizione di limite

Introduzione al concetto di limite di funzione in un punto

Per calcolare il limite, in un  punto di accumulazione, di una funzione si deve studiare il comportamento della funzione nell'intorno di quel punto.

Consideriamo, ad esempio, il grafico della funzione: \( y=\dfrac{k}{x} \)

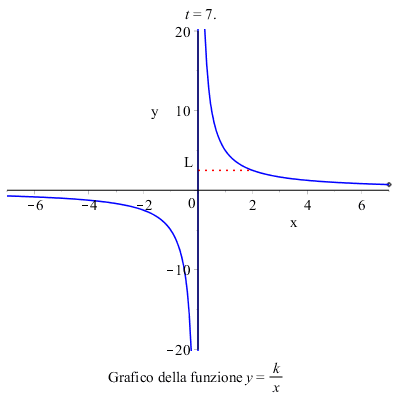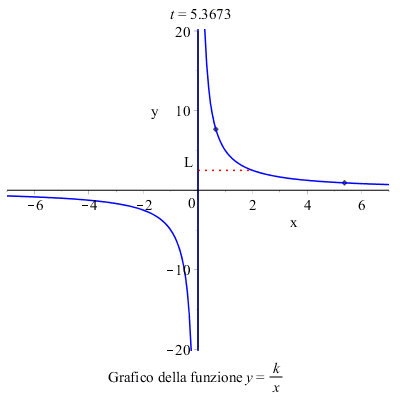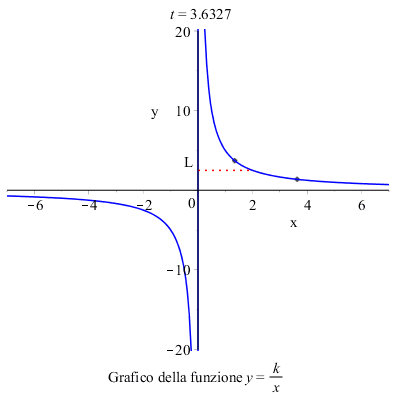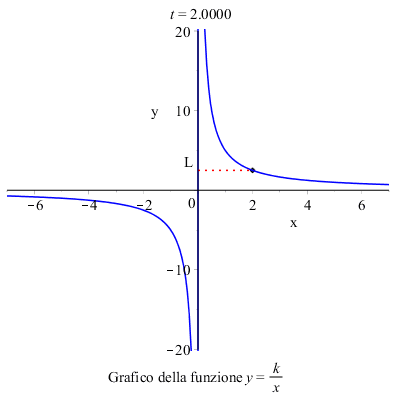
Per calcolare il limite per \( x \) tendente a \( 2 \) della funzione focalizziamo l'attenzione sui valori che la funzione assume in un intorno di \( 2 \), e concludiamo che il limite della funzione per \( x \rightarrow 2 \) esiste e vale \( L \) .

Proviamo adesso a considerare la stessa funzione privata del punto \( A=(2,L) \):

\( y = \begin{cases} \dfrac{k}{x} \quad x<2 \\ \dfrac{k}{x} \quad x>2 \end{cases} \)

Questo significa che quando l'ascissa vale \( 2 \) non esiste alcun valore per la funzione.

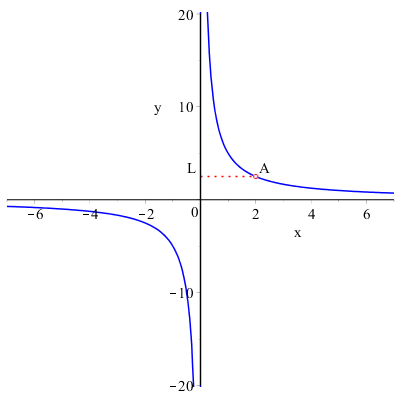
La funzione non è definita in \( x=2 \) tuttavia nell'intorno destro e sinistro di \( 2 \) la funzione assume un valore molto vicino  a \( L \),  allora diciamo che il limite della funzione per \( x \rightarrow 2 \) esiste e vale ancora \( L \).

Proviamo un'ultima variante della funzione di partenza togliendo il punto \( A(2,L) \) e aggiungendo il punto \( B(2,10) \):

\( y= \begin{cases} \dfrac{k}{x} \quad x < 2 \\ 10 \quad x = 2\\ \dfrac{k}{x} \quad x>2 \end{cases} \)

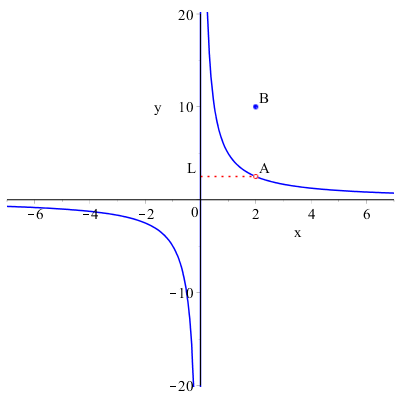
La funzione è definita in \( x=2 \) dove assume il valore \( 10 \) ma analizzando il comportamento della funzione nell'intorno destro e sinistro di \( 2 \), diciamo che il limite   esiste e vale ancora \( L \).

Calcolare il limite di una funzione in un punto significa quindi valutare il suo comportamento non nel punto ma nell'intorno del punto.