1.1 Definizione di limite
1. Definizione di limite
1.2. Definizione limite infinito al finito
Si dice che la funzione \( y=f(x) \) tende a infinito per \( x \) che tende ad \( a \in \mathbb{R} \) e si scrive\( \displaystyle \lim_{x \to a}{f(x)}= \infty \)
se per qualsiasi numero reale \( M>0 \) esiste un numero reale \( \delta > 0 \), tale per cui per ogni \( x \) appartenente all'intervallo \( ]a-\delta,a+\delta[ \) si ha \( |f(x)|>M \); ovvero \( f(x) \) si avvicina arbitrariamente a \( \infty \) a patto di prendere \( x \) sufficientemente vicino a \( a \).
In tale caso, la retta \( x=a \) è un asintoto verticale per il grafico della funzione.
\( \displaystyle \lim_{x \to 2}{\left |\dfrac{3x}{x-2} \right |}=+\infty \)
scegliamo un valore \( M \) arbitrariamente grande sull'asse \( y \) e osserviamo che i punti della funzione che superano questo valore hanno le loro ascisse all'interno di un intorno di \( 2 \) sull'asse \( x \).
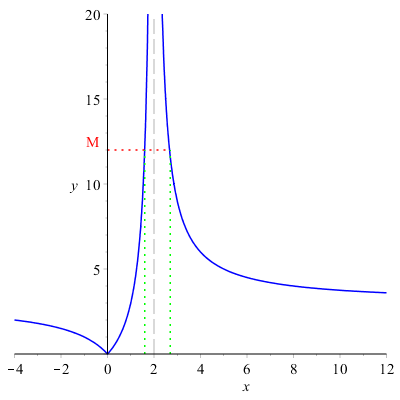
Scegliendo per \( M \) un valore sempre più grande i punti della funzione che sono maggiori di M continuano ad avere le loro ascisse in un intorno di \( 2 \).
Osservazione: il valore 2 è escluso perché non appartiene al dominio della funzione, e poichè il limite per \( x \) tendente a \( 2 \) è infinito, la retta \( x=2 \) è un asintoto verticale.
Bisogna tenere presente che se una funzione non è definita in un punto, non necessariamente ha in quel punto un asintoto verticale.