1.1 Definizione di limite

Si dice che la funzione \(y=f(x) \), per \( x \) tendente ad  \( a \) da sinistra (o da destra), ha il limite sinistro (o destro) e si scrive

\( \displaystyle \lim_{x \to a^-}{f(x)}=l \)    \( \displaystyle \left ( \lim_{x \to a^+}{f(x)}=l \right ) \)

se per ogni intorno di \( l \) di raggio \( \epsilon \) esiste un intorno sinistro (o destro) di \( a \) di raggio \( \delta \) tale che, comunque scelto nell'intorno di \( a \) un valore \( x \) appartenente al dominio e diverso da \(a \), il corrispondente valore \( f(x) \) cade nell'intorno di \( l \); ovvero, \( f(x) \) si avvicina arbitrariamente a \( l \) a patto di prendere \( x \) sufficientemente vicino ad \( a \) da sinistra (o da destra).

Se una funzione ha in un punto un limite finito, allora in quel punto il limite destro e il limite sinistro coincidono. Può accadere tuttavia che, in un punto, una funzione abbia soltanto il limite sinistro (oppure solo il destro), oppure che il limite sinistro e quello destro esistano entrambi, ma non coincidano. 

Ad esempio, se consideriamo il grafico della funzione:

\( \displaystyle f(x)= \begin{cases} 1 \quad x \geq 0 \\ -1 \quad x<0 \end{cases} \)

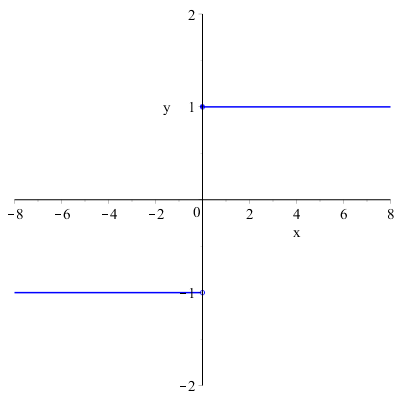
Si può notare che, quando la \( x \) si avvicina a \( 1 \) da destra, la funzione tende al valore \( y=1 \), mentre quando la \( x \) si avvicina a \( 1 \) da sinistra la funzione tende al valore \( y=-1 \), ovvero:

\( \displaystyle \lim_{x \to 1^-}{f(x)}=-1 \)     e      \( \displaystyle \lim_{x \to 1^+}{f(x)}=1 \)

In tale caso la funzione non ha limite per \( x \) tendente a \( 1 \), dato che il limite sinistro e destro non coincidono.