Stampa questo capitoloStampa questo capitolo

1.1 Frazioni

1.3 Frazioni equivalenti

Si dicono equivalenti le frazioni che rappresentano la stessa parte dell'intero. 

\(\frac{1}{2}\) \(\frac{2}{4}\)
 \(\frac{3}{6}\)
 \(\frac{4}{8}\)
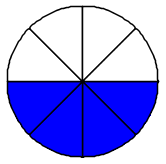La figura mostra un cerchio diviso in due parti uguali, di cui una è evidenziata. La figura mostra un cerchio diviso in 4 parti uguali, di cui 2 sono evidenziate. La figura mostra un cerchio diviso in 6 parti uguali, di cui 3 sono evidenziate. La figura mostra un cerchio diviso in 8 parti uguali, di cui 4 sono evidenziate.

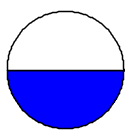
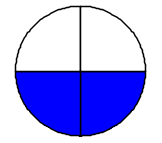
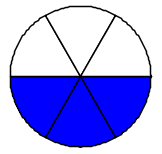
Le frazioni \(\frac{2}{4}\), \(\frac{3}{6}\) e \(\frac{4}{8}\) sono tutte equivalenti a \(\frac{1}{2}\). Frazioni equivalenti si ottengono moltiplicando o dividendo sia il numeratore sia il denominatore di una frazione per uno stesso numero diverso da zero.

Ci sono infinite frazioni equivalenti ad una data frazione. Questo significa che ci sono infiniti modi per esprimere la stessa frazione, come nei disegni sopra: tutte le frazioni scritte indicano la stessa "quantità di torta", la stessa porzione della figura intera. In genere si preferisce rappresentare la frazione ridotta ai minimi termini, cioè quando numeratore e denominatore non hanno divisori comuni. 

Per ridurre una frazione ai minimi termini è necessario dividere sia il numeratore sia il denominatore per il loro massimo comune divisore.