2.2 Risolvere un'equazione

Consideriamo un'equazione di primo grado in un'incognita, ad esempio: 

\( 3x-5 = 7-x \)

Considerando separatamente i due membri, ciascuno di essi può essere descritto come funzione di \( x \), cioè le due espressioni \( 3x-5 \) e \( 7-x \) assumono valori diversi quando si sostituisce un diverso numero alla \(x \). In particolare entrambe possono essere rappresentate graficamente come due rette: 

\( y = 3x-5 \quad \text{e} \quad y = 7-x \)

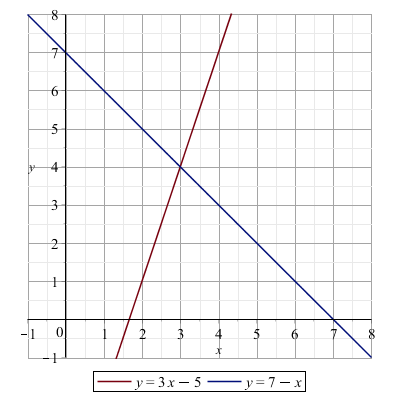
La soluzione dell'equazione è il valore di \( x \) per cui le due rette si incontrano. 

In questo caso la soluzione dell'equazione è  \( x=3 \) . Quando si sostituisce tale valore nell'equazione si ottiene l'identità  \( 4=4 \), che corrisponde all'ordinata del punto di intersezione delle due rette.