3.1 Le funzioni
1.3 Tabelle e grafici
Per esaminare la relazione che intercorre tra due grandezze variabili, si può ricorrere all'esame di una tabella nella quale sono riportati i valori assunti dalle variabili, oppure si può più semplicemente ricorrere ad un grafico che mostra immediatamente il tipo di relazione che intercorre tra le due variabili e che è più facile a leggersi e più conciso.
Tornando all'esempio del paragrafo 1.2, esprimiamo la spesa totale y dei tre amici in funzione del prezzo x del biglietto tramite la formula y=3⋅x+6 .
Per rappresentarla possiamo utilizzare una tabella:
| Variabile indipendente x |
Variabile dipendente y |
|---|---|
| 10 | y=3⋅10+6=36 |
| 15 | y=3⋅15+6=51 |
| 20 | y=3⋅20+6=66 |
In alternativa, possiamo utilizzare un grafico per rappresentare la funzione y=3⋅x+6 :
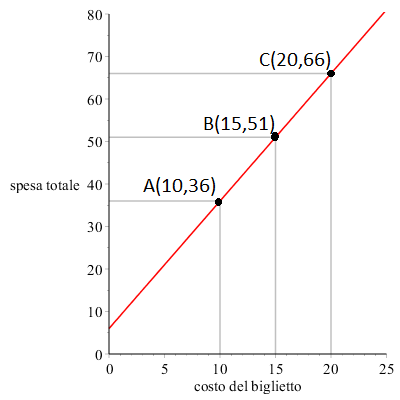
Per tracciarlo abbiamo disegnato i punti A, B, C calcolati precedentemente e li abbiamo quindi congiunti con una retta.
Sapevamo già a priori che il grafico sarebbe stato una retta in quanto la formula matematica che lega le nostre variabili è una funzione lineare (ovvero di primo grado).