Stampa libroStampa libro

1.1 Frazioni

Sito: E-Learning PP&S
Corso: Classe Prima - AI4 - Istituto Tecnico Industriale e Telecomunicazioni 4 anni
Libro: 1.1 Frazioni
Stampato da: Utente ospite
Data: domenica, 28 aprile 2024, 08:02

Descrizione

Teoria sulle frazioni

Sommario

1.1 Le frazioni

Una frazione è un operatore che permette di dividere l'intero in parti uguali e considerarne alcune di esse.  

La scriviamo nella forma: \( \frac{m}{n} \), dove m è il numeratore, n è il denominatore, la linea che li separa si chiama linea di frazione. Più esattamente possiamo dire che:

Una frazione  \( \frac{m}{n} \), dove  m ed n sono numeri interi, con \(n \neq 0\), è un operatore che permette di dividere l'unità in n parti uguali, e considerarne m.

Ecco alcune frazioni, con una loro rappresentazione grafica: 


\( \frac{3}{8} \)

\( \frac{1}{4} \)

\( \frac{5}{3} \)
    L'immagine mostra un rettangolo diviso in otto parti uguali, di cui tre sono colorate.              L'immagine mostra un cerchio diviso in quattro parti uguali, di cui una è colorata.           L'immagine mostra rettangoli uguali, suddivisi in tre parti uguali, di cui sono evidenziate cinque. Bisogna considerare due rettangoli.     





1.2 Calcolare la frazione di una grandezza

Per calcolare una frazione \(\frac{m}{n}\) di una grandezza bisogna compiere due operazioni:  

  1. Dividere la grandezza in n parti uguali
  2. Considerare m delle parti precedentemente divise. 


Ad esempio per calcolare i \(\frac{3}{5}\) del segmento AB dobbiamo: 

  1. Suddividere il segmento AB in 5 parti uguali
  2. Selezionare 3 delle 5 parti in cui il segmento è stato suddiviso.

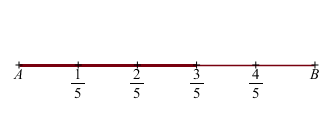
L'immagine mostra un segmento suddiviso in 5 parti, di cui 3 sono evidenziate.

Supponiamo che il segmento AB sia lungo 20 cm. Per calcolare la lunghezza del segmento AC, che misura i \(\frac{3}{5}\)  di AB, dobbiamo: 

  1. Dividere la lunghezza di AB, cioè 20 per 5, per trovare la lunghezza di ogni parte
    20 : 5 = 4
  2. Moltiplicare la lunghezza di ogni parte appena calcolata, cioè 4, per 3, che è il numero di parti che vogliamo considerare
    4 x 3 = 12
AC è lungo 12 cm. Abbiamo calcolato \( \frac{3}{5} \cdot 20 = 12 \)


1.3 Frazioni equivalenti

Si dicono equivalenti le frazioni che rappresentano la stessa parte dell'intero. 

\(\frac{1}{2}\) \(\frac{2}{4}\)
 \(\frac{3}{6}\)
 \(\frac{4}{8}\)
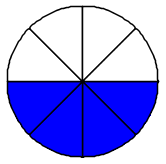La figura mostra un cerchio diviso in due parti uguali, di cui una è evidenziata. La figura mostra un cerchio diviso in 4 parti uguali, di cui 2 sono evidenziate. La figura mostra un cerchio diviso in 6 parti uguali, di cui 3 sono evidenziate. La figura mostra un cerchio diviso in 8 parti uguali, di cui 4 sono evidenziate.

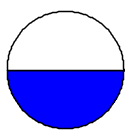
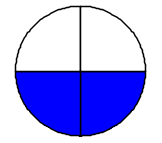
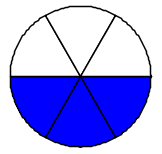
Le frazioni \(\frac{2}{4}\), \(\frac{3}{6}\) e \(\frac{4}{8}\) sono tutte equivalenti a \(\frac{1}{2}\). Frazioni equivalenti si ottengono moltiplicando o dividendo sia il numeratore sia il denominatore di una frazione per uno stesso numero diverso da zero.

Ci sono infinite frazioni equivalenti ad una data frazione. Questo significa che ci sono infiniti modi per esprimere la stessa frazione, come nei disegni sopra: tutte le frazioni scritte indicano la stessa "quantità di torta", la stessa porzione della figura intera. In genere si preferisce rappresentare la frazione ridotta ai minimi termini, cioè quando numeratore e denominatore non hanno divisori comuni. 

Per ridurre una frazione ai minimi termini è necessario dividere sia il numeratore sia il denominatore per il loro massimo comune divisore.