5.3 Quadrilateri
| Site: | E-Learning PP&S |
| Course: | Classe Prima - AI4 - Istituto Tecnico Industriale e Telecomunicazioni 4 anni |
| Book: | 5.3 Quadrilateri |
| Printed by: | Utente ospite |
| Date: | Tuesday, 8 April 2025, 10:52 PM |
Description
Qui troverai le definizioni e le principali proprietà dei quadrilateri.
Il quadrilatero
Un quadrilatero è un poligono avente 4 lati e 4 angoli.

La somma degli angoli interni di un quadrilatero è sempre uguale a 360°.
3.2 Classificazione dei quadrilateri
I quadrilateri si possono classificare a seconda del rapporto di parallelismo tra i loro lati opposti.
| Quadrilatero generico | nessuna coppia di lati paralleli | 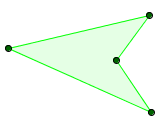 |
|---|---|---|
| Trapezio | una coppia di lati paralleli | 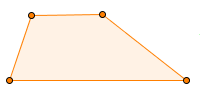 |
| Parallelogramma | due coppie di lati paralleli | 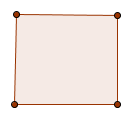 |
Trapezi
I trapezi sono quadrilateri aventi una coppia di lati paralleli. Si possono ancora classificare in:
| Trapezio isoscele |
|
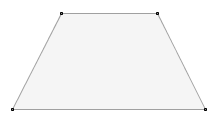 |
|---|---|---|
| Trapezio rettangolo |
|
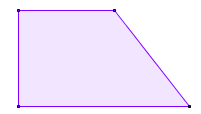 |
| Trapezio scaleno |
|
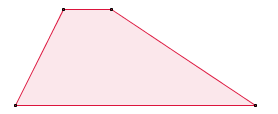 |
Perimetro del trapezio
Il perimetro del trapezio si calcola sommando le misure dei lati
\( P = a + b + c + d \) 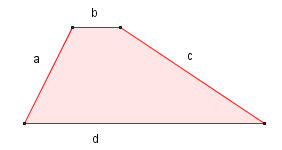
Area del trapezio
L'area del trapezio si calcola moltiplicando la somma delle lunghezze dei lati paralleli per l'altezza e dividendo il risultato per due.
\( A = \frac{(b+d) \cdot h}{2} \)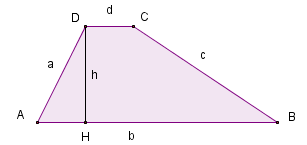
Parallelogrammi
I parallelogrammi sono quadrilateri aventi i lati a due a due paralleli. Si possono ancora classificare in:
| Perimetro | Area | |||
| Rettangoli | Hanno tutti gli angoli uguali (retti) | 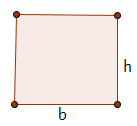 | \( P = 2 \cdot (b + h) \) | \( A = b \cdot h \) |
| Quadrati | Hanno tutti gli angoli uguali e tutti i lati uguali | 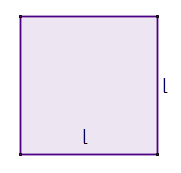 | \(P = 4 \cdot l \) | \(A = l^2 \) |
| Rombi | Hanno tutti i lati uguali | 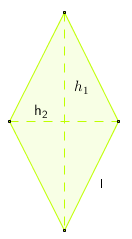 | \( P = 4 \cdot l \) | \( A = \frac{h_1 \cdot h_2}{2} \) |
| Parallelogrammi generici | Hanno lati e angoli uguali a due a due | 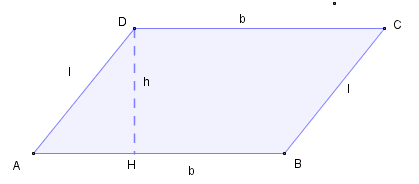 | \( P = 2 \cdot (b + l) \) | \( A = b \cdot h \) |