6.1 Logica
| Sito: | E-Learning PP&S |
| Corso: | Classe Prima - AI4 - Istituto Tecnico Industriale e Telecomunicazioni 4 anni |
| Libro: | 6.1 Logica |
| Stampato da: | Utente ospite |
| Data: | giovedì, 1 maggio 2025, 11:23 |
Descrizione
Qui troverai appunti sulle proposizioni logiche e le relazioni.
1.1 Proposizioni logiche
Una proposizione logica è una frase di senso compiuto per la quale si può stabilire indiscutibilmente se è vera o falsa.
Ad esempio sono proposizioni logiche:
| sono sicuramente vere |
|---|---|
| sono sicuramente false |
Mentre NON sono proposizioni logiche
|
non ha senso stabilire se sono vere o false |
|---|---|
|
è un giudizio personale, non è certamente vero o falso |
Per ogni proposizione logica possiamo dunque stabilire il valore di verità, cioè VERO oppure FALSO, e si indicano con V e F. Scriviamo:
p:″...″ per indicare una proposizione
p=V se la proposizione è vera
p=F se la proposizione è falsa
Ad esempio:
p1:13 è un numero primo p1=V |
p2:Il cerchio ha 5 lati p2=F |
|---|
1.2 Connettivi logici
Le proposizioni logiche viste nel paragrafo precedente si dicono proposizioni semplici: ciascuna fornisce una sola informazione. Le proposizioni semplici possono essere legate tra di loro da congiunzioni, come "e", "ma", "allora": le proposizioni così formate si dicono proposizioni composte.
La logica si occupa di analizzare le proposizioni semplici e assegnare loro un valore di verità, cioè stabilisce se sono vere o false. Sulla base di questi si assegna un valore di verità alle proposizioni composte.
Le particelle mediante le quali si collegano due proposizioni si chiamano connettivi logici: tra di essi distinguiamo la congiunzione, la disgiunzione, la negazione, l'implicazione.
La congiunzione logica
Il connettivo "e" si dice congiunzione logica e si indica con il simbolo \( \wedge \). Consideriamo ad esempio le proposizioni:
\( p: \: \text{Maria ha i capelli castani.} \)
\( q: \: \text{Maria ha gli occhi verdi.} \)
La congiunzione di queste frasi sarà:
\( p \wedge q: \: \text{Maria ha i capelli castani e gli occhi verdi.} \)
Tale affermazione è vera solo se sono vere entrambe le proposizioni di cui è composta: cioè se Maria ha sia i capelli castani sia gli occhi verdi. Nel caso in cui anche una sola delle due proposizioni non sia più vera, ad esempio se Maria avesse gli occhi azzurri, allora non sarebbe vera la proposizione composta "Maria ha i capelli castani e gli occhi verdi". Possiamo schematizzare tutti i casi possibili in una tabella:
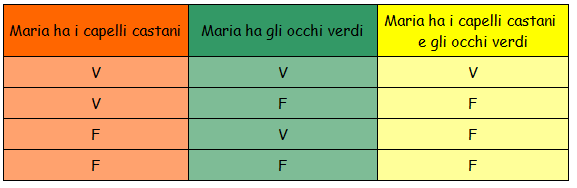
In generale, una proposizione composta con la congiunzione "e" è vera solo se entrambe le proposizioni che la compongono sono vere.
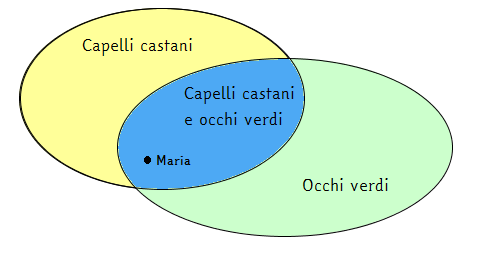
Se dovessimo collocare Maria nell'insieme di tutte le persone conoscendo le caratteristiche "occhi verdi" e "capelli castani", Maria appartiene sia all'insieme delle persone con gli occhi verdi, sia all'insieme delle persone con i capelli castani, quindi la troviamo nell'intersezione di tali insiemi.
Disgiunzione logica
Il connettivo "o" si dice disgiunzione logica e si indica con il simbolo \( \vee \). Consideriamo ad esempio le proposizioni:
\( p: \: \text{Francesco guarda la televisione.} \)
\( q: \: \text{Francesco mangia un gelato .} \)
La disgiunzione di queste frasi sarà:
\( p \vee q: \: \text{Francesco guarda la televisione o mangia un gelato.} \)
Tale affermazione è vera se è vera almeno una delle proposizioni di cui è composta: cioè se Francesco guarda la televisione oppure se Francesco mangia un gelato, e a maggior ragione è vera se sono vere entrambe. Invece non è vera se Francesco non sta nè guardando la TV nè mangiando un gelato. Possiamo schematizzare tutti i casi possibili in una tabella:
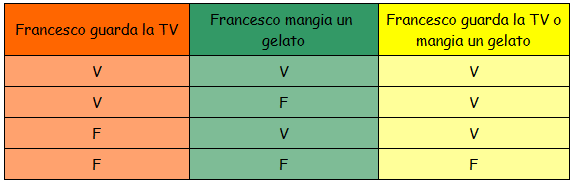
In generale, una proposizione composta con la disgiunzione "o" è vera se almeno una delle proposizioni che la compongono è vera.
Se dovessimo collocare Francesco nell'insieme di tutte le persone che stanno compiendo qualche azione, potremmo trovarlo o nell'insieme delle persone che guardano la TV, o nell'insieme delle persone che mangiano un gelato, o nella loro intersezione, quindi nell'unione dei due insiemi.
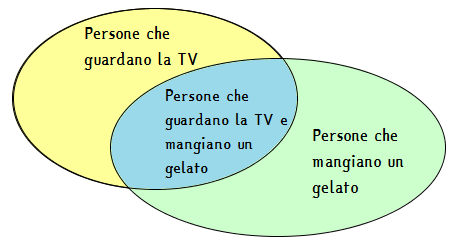
Francesco potrebbe collocarsi in una qualsiasi delle parti colorate di questi insiemi.
Negazione logica
Il connettivo "non" si dice negazione logica e si indica con il simbolo \( \neg \). Consideriamo ad esempio le proposizioni:
\( p: \: \text{Parigi è in Francia.} \)
La negazione di questa frase sarà:
\( \neg p: \: \text{Parigi non è in Francia.} \)
Tale proposizione è ovviamente falsa, poichè è vero che Parigi è in Francia; se la proposizione \( p \) fosse falsa, allora sarebbe vera la sua negazione. Possiamo schematizzare tutti i casi possibili in una tabella:
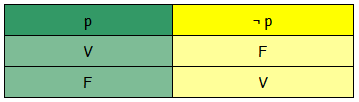
In generale, una proposizione negata dalla negazione "non" è vera se la proposizione originale è falsa e viceversa.
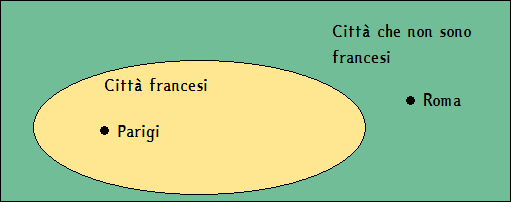
Dovendo collocare Parigi tra tutte le città del mondo, la inseriamo tra le città francesi; Roma invece, poichè è vera la proposizione "Roma non è in Francia", la collochiamo al di fuori dell'insieme delle città francesi (cioè nel complementare dell'insieme delle città francesi rispetto a tutte le città del mondo).
L'implicazione logica
Consideriamo la proposizione:
"Se vieni a casa, allora ti potrò far leggere la ricerca"
Questa rappresenta una proposizione composta da due proposizioni unite fra loro dai connettivi logici "se... allora"; nel suo insieme si può verificare solo se si verifica la prima delle due proposizioni ("andare a casa") che rappresenta la condizione affinché la seconda ("leggere la ricerca") si possa verificare.
I connettivi "se...allora", "...quindi", "... perciò" si dicono implicazioni logiche; la proposizione composta che utilizza questi connettivi si chiama implicazione ed il suo simbolo matematico è \( \Rightarrow \) e si legge "implica".
Per esempio consideriamo le proposizioni:
p: "Mario è torinese" q: "Mario è italiano"
la proposizione \( p \Rightarrow q \) sarà: "Mario è torinese quindi è italiano"
è evidente da questo esempio che:
- \( p \Rightarrow q \) è vera solo se, essendo vera p, risulta vera anche q
- Non è detto che la relazione di implicazione sia invertibile, ovvero da \( p \Rightarrow q \) NON segue necessariamente \( q \Rightarrow p \)
Riprendendo l'esempio, infatti, è sicuramente vero che "Se Mario è torinese allora è italiano" ( \( p \Rightarrow q \) ) mentre non è detto che sia vero "Se Mario è italiano allora è torinese" (\( q \Rightarrow p \))
Quando invece è vera \( p \Rightarrow q \) ed è vera anche \( q \Rightarrow p \) si parla di doppia implicazione logica; si scrive \( p \Leftrightarrow q \) dove il simbolo \( \Leftrightarrow \) si legge "se e solo se"
Ad esempio consideriamo le proposizioni:
p: "12 è un numero pari" q: "12 è divisibile per 2"
\( p \Rightarrow q \) : "12 è un numero pari quindi è divisibile per 2" è vera
ma anche
\( q \Rightarrow p \) : "12 è un numero divisibile per 2 quindi è pari" è vera
si tratta quindi di una coimplicazione che possiamo riscrivere come:
\( p \Leftrightarrow q \) : "12 è un numero pari se e solo se è divisibile per due"