1.1 Probabilità
| Sito: | E-Learning PP&S |
| Corso: | Classe Terza - AL4 - Liceo Internazionale Scienze Applicate 4 anni |
| Libro: | 1.1 Probabilità |
| Stampato da: | Utente ospite |
| Data: | martedì, 6 maggio 2025, 13:32 |
Descrizione
Prob
1. Introduzione e terminologia: lo spazio campionario e gli eventi
Parlando di probabilità vengono in mente i giochi di carte, il lancio di dadi o di monete. Nello specifico il calcolo delle probabilità ha come oggetto di studio gli esperimenti casuali, di cui a priori non si conosce il risultato. Con la proposizione “La probabilità che succeda una certa cosa è..” diamo l’impressione a chi ci ascolta che esista una ed una sola definizione di probabilità mentre non è così. Quando il Calcolo delle Probabilità cominciò a svilupparsi le opinioni degli studiosi cominciarono a divergere e si vennero a creare concezioni diverse di probabilità, come ad esempio la concezione classica, frequentista o soggettivista.
Prima di vedere le varie concezioni di probabilità è necessario dare la definizione di evento. Con il termine evento si intende un qualsiasi fatto o avvenimento che può essere osservato e descritto da un enunciato, come ad esempio “È uscito il 3 nel lancio di un dato”. È importante evitare ogni ambiguità nella definizione di un evento, ovvero è necessario che sia possibile una sola delle conclusioni: l'evento si è verificato, cioè l'enunciato è vero, l'evento non si è verificato, cioè l'enunciato è falso. Si possono avere eventi certi, impossibili o casuali (aleatori).
Il calcolo delle probabilità si occupa di
studiare gli eventi aleatori, infatti nell’ambito di questi si possono
distinguere eventi che hanno maggiori possibilità di verificarsi rispetto ad
altri. Associamo allora ad ogni evento un numero reale, che è tanto maggiore quanto più è elevata la possibilità che si verifichi
l’evento stesso, e chiamiamo tale numero probabilità dell’evento (che come
vedremo sarà compreso tra 0 e 1).
Esempio: Se una scatola contiene palline bianche e nere, l’estrazione di una pallina nera è un evento possibile ma non certo, cosi come l’estrazione di una pallina bianca. In altre parole, non possiamo prevedere il colore della pallina estratta, perché l’estrazione è casuale, inoltre se nella scatola ho più palline nere che palline bianche avremo più possibilità di estrarne una nera.
Si dice spazio campionario l’insieme di tutti i possibili esiti o risultati di un esperimento. Di conseguenza un evento sarà un qualsiasi sottoinsieme dello spazio campionario, e rappresenterà quindi un insieme di possibili risultati. Si parla di evento elementare quando questo insieme è costituito da un solo elemento, di evento certo quando l’insieme contiene tutti i possibili risultati, di evento impossibile, rappresentato dall’insieme vuoto.
Operazioni con gli eventi
Dal momento che gli eventi sono insiemi, si possono utilizzare le operazioni tra insiemi anche tra gli eventi.
Dati due eventi E1 ed E2 avremo:
- l’unione di due eventi (E1∪E2) che rappresenta l’evento “si verifica E1 oppure si verifica E2” o, in altre parole, si verifica almeno uno dei due eventi;
- l’intersezione dei due eventi (E1∩E2) che rappresenta l’evento “si verifica contemporaneamente E1 ed E2” ossia si verificano entrambi gli eventi. Quando l’intersezione di due eventi è l’insieme vuoto i due eventi si dicono incompatibili o mutuamente esclusivi ed è impossibile che si verifichino contemporaneamente.
- la differenza tra due eventi (E1–E2) che rappresenta l’evento “si verifica E1 ma non E2”;
- il complementare di un evento (¯E1) che rappresenta l’evento “non si realizza E1”.
Esempio
Un esempio di esperimento di cui non si conosce a priori il risultato è il lancio di un dado.
Lo spazio campionario di tutti i possibili risultati è rappresentato dall’insieme 1,2,3,4,5,6.
Un evento E1 può essere “esce un numero pari”, rappresentato dall’insieme 2,4,6.
Un altro evento E2 può essere “esce un numero maggiore di 4”, rappresentato dall’insieme 5,6.
L’intersezione dei due eventi è l’evento “esce un numero pari maggiore di 4”: E1∩E2=6.
Il complementare dell’evento E1 è “esce un numero dispari”, mentre il complementare dell’evento E2 è “esce un numero minore o uguale a 4”.
2. La definizione classica di probabilità
La concezione classica è la più adatta ad un primo approccio
alla probabilità. Essa dà luogo a una probabilità "a priori" cioè
prima che l'evento si verifichi. Definiamo la probabilità di un evento come il rapporto fra il numero
degli esiti favorevoli, che fanno sì che l’evento si
verifichi, e il numero degli esiti possibili.
Indichiamo la probabilità \(p\) di un evento \(E\) con i simboli:
\(p(E) = \dfrac{n° esiti favorevoli}{n° esiti possibili}\)
Il numero di esiti favorevoli corrisponde al numero di elementi dell’insieme che rappresenta l’evento \(E\); mentre il numero di esiti possibili corrisponde al numero di elementi dello spazio campionario.
La condizione che deve essere verificata è che tutti gli esiti siano ugualmente possibili, ossia che nessun esito possa verificarsi più facilmente di un altro.
Alcune osservazioni
- Se \(E\) è un evento certo allora \(p(E) = 1\): l’evento certo
infatti corrisponde allo spazio campionario.
- Se \(E\) è un evento impossibile allora \(p(E) = 0\): l’evento impossibile infatti corrisponde all’insieme vuoto.
In ogni altro caso la probabilità di un evento \(E\) è un valore compreso tra \(0\) ed \(1\).
In generale quindi vale:
\(0 ≤ p(E) ≤ 1\)
A volte la probabilità si esprime in forma percentuale (ottenuta moltiplicando per \(100\)); il suo valore sarà quindi compreso sempre tra \(0\) e \(100\).
La definizione classica di probabilità non è l’unica
esistente. Ad esempio altre concezioni di probabilità sono:
- La concezione frequentista: secondo la quale la probabilità è la frequenza relativa (quando il
numero delle prove è sufficientemente alto).
Esempio: sappiamo che in un’urna ci sono 100 palline di forma uguale, e alcune di esse (non si quante) sono bianche. Estraiamo una pallina, che può essere bianca o meno, la rimbussoliamo e rimescoliamo il tutto, e così via per 1000 volte. Se supponiamo di aver estratto 703 palline bianche diremo che la frequenza relativa, e quindi la probabilità di estrarre una pallina bianca, è 703/1000 (70.3%).
Con questa concezione abbiamo una probabilità a posteriori.
- La concezione soggettivista: secondo la quale la probabilità è definita come la misura del grado di
fiducia che un soggetto attribuisce all’avverarsi di un evento. Essa
si può esprimere in termini di scommessa: sono disposto a pagare 3 euro di
scommessa sulla Juventus vincente se riceverò 10 euro in caso di una sua
vittoria, mentre se la Juventus perde non riceverò nulla. Allora vuol dire che
do la Juventus vincente con una probabilità del 30% (3/10).
Esiste inoltre una teoria assiomatica che fonda il calcolo della probabilità si un sistema di assiomi, che qui non presentiamo nel dettaglio.
Esempio
Riprendiamo l’esempio del lancio di un dado.
Dire qual è la probabilità che:
1) esca un numero pari
2) esca un numero maggiore di \(4\)
Ricordiamo che:
lo spazio campionario di tutti i possibili risultati è rappresentato dall’insieme \( \lbrace{1, 2, 3, 4, 5, 6}\rbrace \);
l’evento \(E_1\) “esce un numero pari” è rappresentato dall’insieme \( \lbrace{2, 4, 6}\rbrace \);
l’evento \(E_2\) “esce un numero maggiore di \(4\)” è rappresentato dall’insieme \( \lbrace{5, 6}\rbrace \).
1) La probabilità di \(E_1\) è:
\( p(E_1) = \dfrac{n° esiti favorevoli}{n° esiti possibili} = \dfrac{3}{6} = 0,5 \)
2) La probabilità di \(E_2\) è:
\( p(E_2) = \dfrac{n° esiti favorevoli}{n° esiti possibili} = \dfrac{2}{6} \simeq 0,33 \)
3. Teoremi sul calcolo della probabilità
Presentiamo alcuni teoremi utili per il calcolo della
probabilità; anche in presenza di eventi complessi, ovvero composti da più eventi
semplici di cui si conosce la probabilità. Ricordiamo che due eventi si dicono incompatibili quando non possono verificarsi simultaneamente in una data prova e per i
quali si ha \( (E_1 ∩ E_2) = Ø \) .
- Se gli eventi non sono incompatibili, ovvero hanno intersezione non vuota, allora la probabilità della loro unione è la somma delle loro probabilità meno la probabilità della loro intersezione:
\( p(E_1 \cup E_2) = p(E_1) + p(E_2) – p(E_1 ∩ E_2) \)
- La probabilità dell’unione di due o più eventi incompatibili è semplicemente la somma delle loro probabilità:
\(p(E_1 \cup E_2) = p(E_1) +
p(E_2)\)
- La
probabilità del complementare di un evento vale uno meno la probabilità
dell’evento stesso:
\(p( \overline{E} ) = 1 – p(E)\)
Ricordiamo inoltre che due eventi si si dicono complementari quando uno è la negazione dell'altro. Può
sembrare una banalità ma può capitare di commettere qualche errore. Ad esempio,
se si chiede il contrario di "Vincere sempre" si può avere come
risposta "Non vincere mai", mentre la riposta corretta è
"Perdere almeno una volta".
- La probabilità condizionata
La probabilità di un evento è un numero che misura il grado di
fiducia che noi abbiamo circa il realizzarsi di questo evento. È naturale
allora che la probabilità di uno stesso evento possa cambiare, se cambiano le
informazioni in nostro possesso. La scrittura \(p(E_1|E_2)\) indica la probabilità dell’evento \(E_1\)
condizionata all’evento \(E_2\), ossia la probabilità che si verifichi \(E_1\) sapendo
che si è già verificato \(E_2\).
La probabilità condizionata è uguale al seguente rapporto:
\( p(E_1|E_2) = \dfrac{p(E_1 ∩ E_2)}{p(E_2)} \)
- L’indipendenza tra eventi
Un altro concetto importante è quello di indipendenza tra eventi: due eventi \(E_1\) ed \(E_2\) sono indipendenti se il verificarsi di uno non influisce sulla probabilità dell’altro.
I due eventi \(E_1\) ed \(E_2\) sono indipendenti se e solo se vale:
\(p(E_1 ∩ E_2) = p(E_1) · p(E_2)\)
ossia la probabilità della loro intersezione è uguale al prodotto delle probabilità dei singoli eventi.
Nel caso di eventi indipendenti si ha:
\( p(E_1|E_2) = \dfrac{p(E_1 ∩ E_2)}{p(E_2)} = \dfrac{p(E_1) · p(E_2)}{p(E_2)} = p(E_1) \)
- La probabilità composta
Nel caso di due eventi dipendenti la probabilità composta è il prodotto della probabilità del primo evento per la probabilità del secondo condizionata al primo:
\( p(E_1 ∩ E_2) = p(E_1) · p(E_2|E_1) \)
Applicando la definizione vista prima, avremo che nel caso di due eventi indipendenti la probabilità composta è il prodotto delle probabilità dei singoli eventi:
\( p(E_1 ∩ E_2) = p(E_1) · p(E_2) \)
Le relazione si possono generalizzare anche a casi in cui ci sono tre o più eventi.
3.1. Esempio di applicazione dei teoremi
PRIMO ESEMPIO
Un’urna contiene 20 palline, di cui 12 bianche e 8 nere.
Si
estraggono due palline, senza reinserire nell’urna la prima estratta.
Qual è la probabilità che siano dello stesso colore?
Si tratta di calcolare la probabilità dell’unione di due eventi incompatibili:
\(E_1\) “le due palline estratte sono entrambe bianche”
\(E_2\) “le due palline estratte sono entrambe nere”
Partiamo dall’evento \(E_1\) “le due palline estratte sono entrambe bianche”. Questo significa che la prima pallina estratta è bianca e che la seconda pallina estratta è bianca. Notiamo la congiunzione “e” che ci suggerisce una intersezione tra i due eventi:
\(E_{11}\) “la prima pallina estratta è bianca”
\(E_{12}\) “la seconda pallina estratta è bianca”
Nel nostro caso i due eventi sono dipendenti in quanto l’estrazione della seconda pallina dipende dalla prima estratta e non reinserita nell’urna e quindi vale:
\( p(E_{11} ∩ E_{12}) = p(E_{11}) · p(E_{12}|E_{11}) = \dfrac{12}{20} · \dfrac{11}{19} = 0,35 = 35 \% \)
\(p(E_{11})\) e \(p(E_{12}|E_{11})\) sono stati calcolati come rapporto tra il numero di esiti favorevoli e il numero di esiti possibili:
- per \(E_{11}\) si hanno \(12\) esiti favorevoli e \(20\) possibili quindi \(p(E_{11}) = \dfrac{12}{20}\)
- per \(E_{12}|E_{11}\) si hanno \(11\) esiti favorevoli e \(19\) possibili quindi \(p(E_{12}|E_{11}) = \dfrac{11}{19} \)
Passiamo all’evento \(E_2\) “le due palline estratte sono entrambe nere”. Si applica lo stesso ragionamento trovando:
\(p(E_2) = 0,15 = 15 \% \)
Lasciamo al lettore la possibilità di sviluppare i passaggi nel dettaglio.
Per rispondere alla domanda iniziale, si calcola la probabilità dell’unione dei due eventi \(E_1\) ed \(E_2\) che abbiamo detto essere incompatibili:
\( p(E_1 \cup E_2) = p(E_1) + p(E_2) = 0,35 + 0,15 = 0,50 = 50 \%\)
In conclusione la probabilità che le due palline estratte dall’urna siano dello stesso colore è del \(50 \% \).
SECONDO ESEMPIO
Determinare la probabilità matematica che una coppia abbia tre figlie femmine
Utilizziamo, ad esempio, un diagramma ad albero per rappresentare i casi possibili in modo da avere un'elencazione grafica di tutti gli elementi dello spazio campione (indichiamo con 1F= primo figlio, 2F=secondo figlio, 3F=terzo figlio).
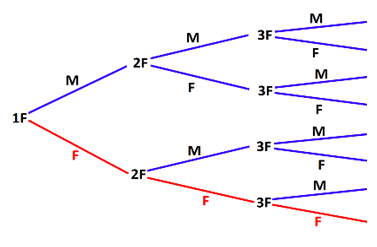
Se scriviamo
su ciascun ramo la probabilità dell'evento rappresentato nel nodo seguente, avremo che la probabilità di uno qualsiasi degli eventi sui rami
terminali è data dal prodotto delle probabilità scritte sull'intero percorso
(questa regola è detta regola del prodotto).
Poichè la probabilità che nasca un figlio maschio o che nasca un figlio femmina è in entrambi i casi uguale a \(\dfrac{1}{2}\), avremo che:
\( p(3F) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2}=\dfrac{1}{8} \)