2.2 La distribuzione normale
| Sito: | E-Learning PP&S |
| Corso: | Classe Terza - AL4 - Liceo Internazionale Scienze Applicate 4 anni |
| Libro: | 2.2 La distribuzione normale |
| Stampato da: | Utente ospite |
| Data: | lunedì, 5 maggio 2025, 16:14 |
Descrizione
distribuzione normale
1. La distribuzione normale
Se si riportano su di un istogramma le frequenze dei dati statistici raccolti e si collegano i punti medi delle basi superiori dei rettangoli si ottiene una linea spezzata; quest'ultima avrebbe una forma a “campana” se si avesse a disposizione un gran numero di dati. La curva teorica che descrive la campana si chiama gaussiana o curva di Gauss, dal grande matematico Karl Friedrich Gauss (1777-1855).La distribuzione Gaussiana è la distribuzione di probabilità che meglio rappresenta molte variabili biologiche, ed è anche la distribuzione di probabilità degli errori casuali e delle statistiche campionarie.
La distribuzione gaussiana o “normale” comprende una famiglia di curve, i cui parametri sono la media μ e la deviazione standard σ.
- La media determina la posizione centrale della curva. La curva, infatti, risulta simmetrica rispetto al valore medio, μ, della distribuzione dei dati.
- La deviazione standard determina l'ampiezza della curva.
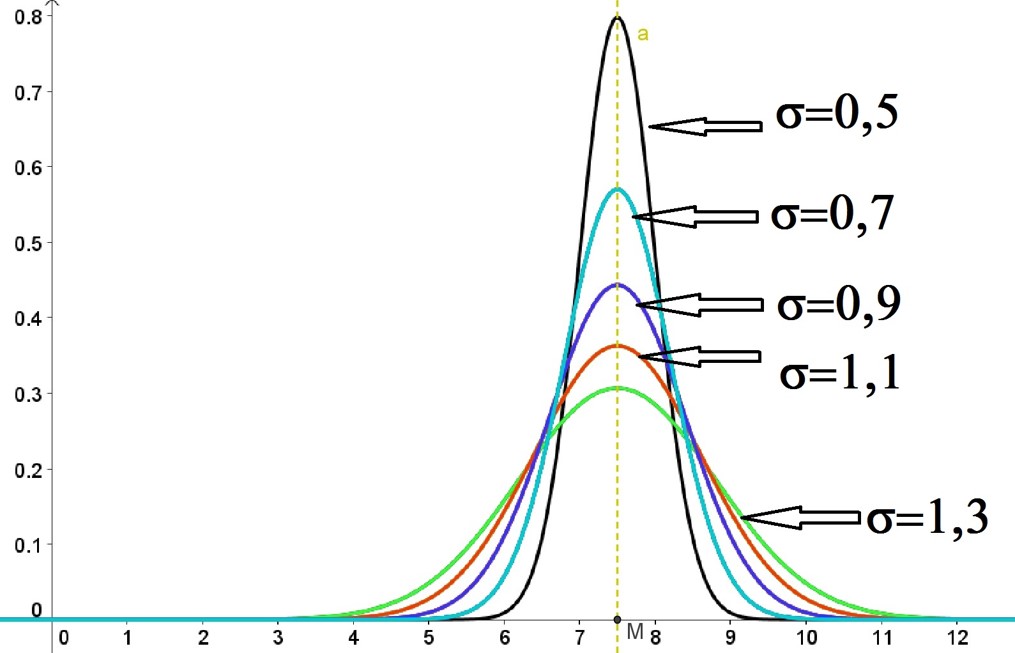
Nel grafico sottostante potete osservare che: - Se la deviazione standard è piccola, la curva è stretta ed allungata. Ciò significa che i dati si addensano attorno al valore medio della distribuzione.
- Se la deviazione standard è grande, la curva si abbassa e si allarga. Ciò significa che i dati si addensano di meno rispetto al valore medio, ovvero i dati si disperdono di più e si allontanano dal valore medio.
Data una variabile la cui distribuzione di probabilità è gaussiana, possiamo misurare la probabilità corrispondente a determinati intervalli di valori della variabile.
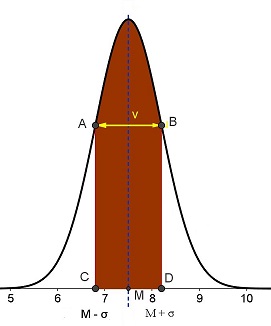
Nel grafico seguente la fascia colorata di marrone sotto la curva gaussiana, che ha per estremi i punti C e D, sta a significare che il 68% dei dati della popolazione indagata si distribuisce tra M–σ e M+σ. I punti C e D hanno rispettivamente ascissa pari a M–σ e M+σ, dove M è la media della distribuzione.
Se invece prendiamo come ascisse dei punti C e D rispettivamente i valori M–2σ e M+2σ, allora la fascia colorata sotto la curva gaussiana che ha per estremi i punti C e D indicherà che il 95% dei dati della popolazione indagata si distribuisce tra M–2σ e M+2σ.
In ultimo, se invece prendiamo come ascisse dei punti C e D i valori M–3σ e M+3σ, allora la fascia colorata sotto la curva gaussiana che ha per estremi i punti C e D indicherà che il 99% dei dati della popolazione indagata si distribuisce tra M–3σ e M+3σ.
2. Esempio
I punteggi assegnati alle prove di un concorso hanno avuto una distribuzione normale e il punteggio medio è stato \(μ=48 \) con una deviazione standard \(σ=12\).Calcoliamo la probabilità:
- che il punteggio sia compreso tra \(39\) e \(43\);
- che il punteggio sia inferiore a \(30\).
Indichiamo con \(X=N(48; 12)\) la variabile casuale normale con una funzione di densità di probabilità normale, che rappresenta i punteggi assegnati. Per semplificare il calcolo, standardizziamo la variabile \(X\) nella variabile \(Z\):
\( Z= \frac{X- \mu }{\sigma} \)
In questo modo abbiamo ottenuto ancora una variabile casuale normale ma con valore medio \(μ=0\) e deviazione standard \(σ=1\). Scriveremo allora \(Z=N(0; 1)\).
Il calcolo della probabilità che la variabile \(N(48; 12)\) assuma un valore compreso tra \(39\) e \(43\), si riconduce al calcolo della probabilità che la variabile \(N(0; 1)\) assuma un valore compreso tra tra \(-0.75\) e \(-0.42\), essendo questi i due valori di \(Z\) corrispondenti ai precedenti. Infatti applicando la relazione:
\( Z= \frac{X- 48}{12} \)
si ha:
\( x_1=39→ z_1=\frac{39- 48}{12}=-0.75 \)
\( x_2=43→ z_1=\frac{43- 48}{12}=-0.42 \)
Si sono approssimati i valori alla seconda cifra decimale.
Esiste una tavola apposita, detta tavola di Sheppard, che fornisce il valore delle aree sottostanti la curva gaussiana \(f(z)\) tra \(0\) e un valore di \(z\), cioè \(F(z)=P(0<Z<z)\). In questa tavola, le righe sono in corrispondenza alla parte decimale del valore \(z\) e le colonne corrispondono ai centesimi. Per esempio, per trovare il valore di \(F(1.35)\) occorre individuare la riga in cui compare il numero \(1.3\) e scorrerla fino alla colonna corrispondente al numero \(0.05\); la casella così individuata contiene il valore cercato. Ricordiamo inoltre che la simmetria della curva gaussiana rispetto l'asse y comporta che la stessa tavola possa essere utilizzata anche per valori negativi della variabile \(Z\), infatti:
\(P(-z<Z<0)=P(0<Z<z)\).
Applichiamo la tavola per trovare il valore cercato:
\(P(-0.75<Z<-0.42)=P(0.42<Z<0.75)=P(0<Z<0.75)-P(0<Z<0.42)=0.2734-0.1628=0.1106\).
Quindi, se trasformiamo il dato in percentuale, la probabilità che il punteggio sia compreso tra \(39\) e \(43\) è l' \(11\%\) circa.
Per risolvere il secondo quesito calcoliamo:
\( x_3=30→ z_1=\frac{30- 48}{12}=-1.5 \)
E di conseguenza avremo:
\(P(-∞<Z<-1.5)=P(1.5<Z<+∞)=P(0<Z<+∞)-P(0<Z<1.5)=0.5-0.4332=0.0668\).
Quindi, se trasformiamo il dato in percentuale, la probabilità che il punteggio sia inferiore a \(30\) è il \(6\%\) circa.