1.1 Definizione di limite
| Site: | E-Learning PP&S |
| Course: | Classe Quarta - 4AL4 - Liceo Internazionale Scienze Applicate 4 anni |
| Book: | 1.1 Definizione di limite |
| Printed by: | Guest user |
| Date: | Friday, 14 March 2025, 1:04 AM |
1. Definizione di limite
Introduzione al concetto di limite di funzione in un punto
Per calcolare il limite, in un punto di accumulazione, di una funzione si deve studiare il comportamento della funzione nell'intorno di quel punto.
Consideriamo, ad esempio, il grafico della funzione: \( y=\dfrac{k}{x} \)
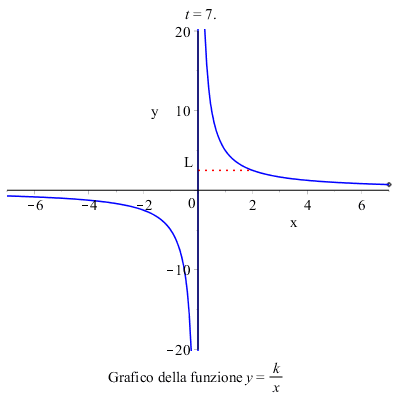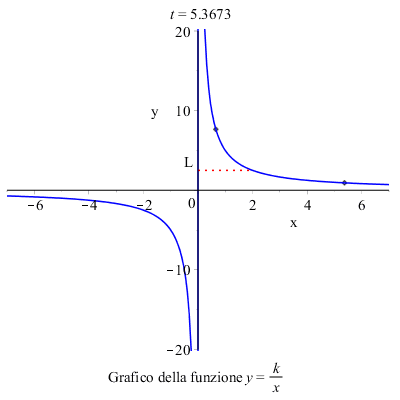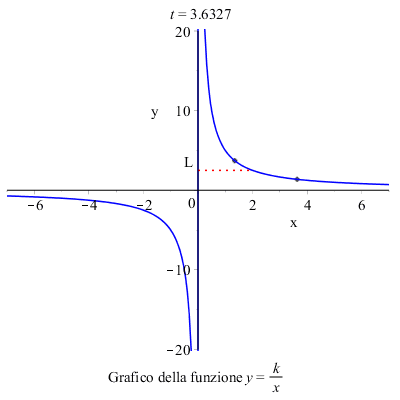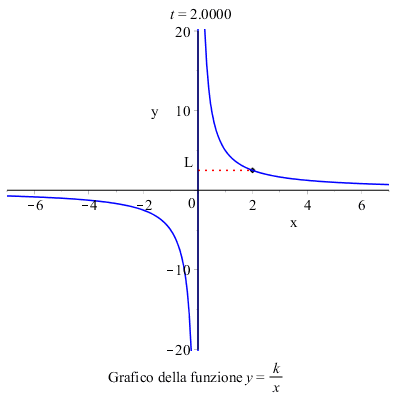
Per calcolare il limite per \( x \) tendente a \( 2 \) della funzione focalizziamo l'attenzione sui valori che la funzione assume in un intorno di \( 2 \), e concludiamo che il limite della funzione per \( x \rightarrow 2 \) esiste e vale \( L \) .
Proviamo adesso a considerare la stessa funzione privata del punto \( A=(2,L) \):
\( y = \begin{cases}
\dfrac{k}{x} \quad x<2 \\
\dfrac{k}{x} \quad x>2
\end{cases} \)
Questo significa che quando l'ascissa vale \( 2 \) non esiste alcun valore per la funzione.
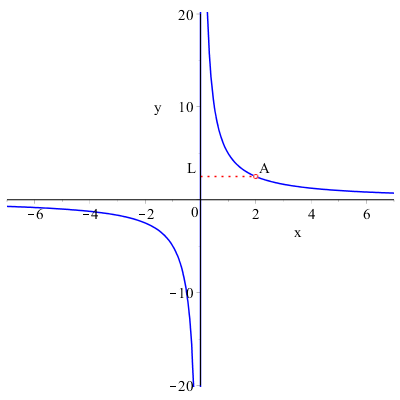
La funzione non è definita in \( x=2 \) tuttavia nell'intorno destro e sinistro di \( 2 \) la funzione assume un valore molto vicino a \( L \), allora diciamo che il limite della funzione per \( x \rightarrow 2 \) esiste e vale ancora \( L \).
Proviamo un'ultima variante della funzione di partenza togliendo il punto \( A(2,L) \) e aggiungendo il punto \( B(2,10) \):
\( y= \begin{cases}
\dfrac{k}{x} \quad x < 2 \\
10 \quad x = 2\\
\dfrac{k}{x} \quad x>2
\end{cases} \)
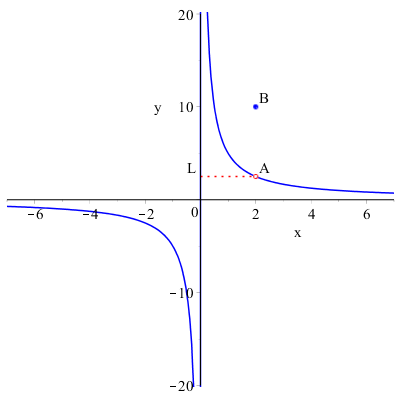
La funzione è definita in \( x=2 \) dove assume il valore \( 10 \) ma analizzando il comportamento della funzione nell'intorno destro e sinistro di \( 2 \), diciamo che il limite esiste e vale ancora \( L \).
Calcolare il limite di una funzione in un punto significa quindi valutare il suo comportamento non nel punto ma nell'intorno del punto.
1.1. Definizione limite finito al finito
Definizione. Si dice che \( l \in \mathbb{R} \) è il limite della funzione \( y=f(x) \) per \( x \) che tende ad \( a \in \mathbb{R} \) e si scrive
\( \displaystyle \lim_{x \to a}{f(x)}=l \)
se per ogni \( \epsilon >0 \) esiste un numero \( \delta >0 \) tale che:
\( \forall x (|x-a| <\delta, x \neq a) \Rightarrow |f(x)-l|<\epsilon \),
ovvero se \( f(x) \) si avvicina arbitrariamente ad \( l \) a patto di prendere \( x \) sufficientemente vicino a \( a \).
Esempio. Dato il seguente limite:
\( \displaystyle \lim_{x \to 4}{\dfrac{3x}{x-2}}=6 \)
Scegliamo sull'asse delle \( y \) un intorno di \( 6 \), ovvero un intervallo aperto di piccole dimensioni \( \left ]6-\epsilon,6+\epsilon \right[ \) e notiamo come questo intorno ne individua uno corrispondente di \( 4 \) sull'asse \( x \).
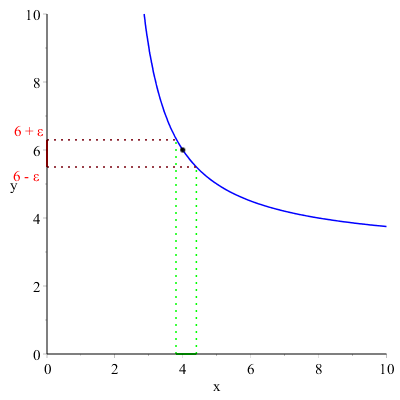
Facendo variare \( \epsilon \), piccolo a piacere e positivo, e di conseguenza l'intorno sull'asse \( y \), i punti della funzione che sono compresi fra le due rette orizzontali hanno le loro ascisse nell'intorno di \( 6 \).
NOTA BENE: La condizione \( x \neq a \) presente nella definizione, sta a significare che nel caso in cui la funzione non esistesse nel punto di ascissa \( a \) o avesse in esso un punto isolato la definizione di limite funziona ugualmente. Quindi il risultato del limite non dà alcuna informazione sul comportamento della funzione nel punto.
1.2. Definizione limite infinito al finito
Si dice che la funzione \( y=f(x) \) tende a infinito per \( x \) che tende ad \( a \in \mathbb{R} \) e si scrive\( \displaystyle \lim_{x \to a}{f(x)}= \infty \)
se per qualsiasi numero reale \( M>0 \) esiste un numero reale \( \delta > 0 \), tale per cui per ogni \( x \) appartenente all'intervallo \( ]a-\delta,a+\delta[ \) si ha \( |f(x)|>M \); ovvero \( f(x) \) si avvicina arbitrariamente a \( \infty \) a patto di prendere \( x \) sufficientemente vicino a \( a \).
In tale caso, la retta \( x=a \) è un asintoto verticale per il grafico della funzione.
\( \displaystyle \lim_{x \to 2}{\left |\dfrac{3x}{x-2} \right |}=+\infty \)
scegliamo un valore \( M \) arbitrariamente grande sull'asse \( y \) e osserviamo che i punti della funzione che superano questo valore hanno le loro ascisse all'interno di un intorno di \( 2 \) sull'asse \( x \).
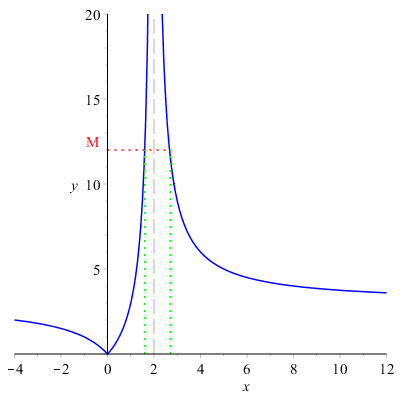
Scegliendo per \( M \) un valore sempre più grande i punti della funzione che sono maggiori di M continuano ad avere le loro ascisse in un intorno di \( 2 \).
Osservazione: il valore 2 è escluso perché non appartiene al dominio della funzione, e poichè il limite per \( x \) tendente a \( 2 \) è infinito, la retta \( x=2 \) è un asintoto verticale.
Bisogna tenere presente che se una funzione non è definita in un punto, non necessariamente ha in quel punto un asintoto verticale.
1.3. Definizione limite finito all'infinito
Definizione. Si dice che \( l \in \mathbb{R} \) è il limite della funzione \( y=f(x) \) per \( x \) tendente all'infinito e si scrive\( \displaystyle \lim_{x \to +\infty}{f(x)}=l \)
se per ogni intorno di \( l \) di raggio \( \epsilon \) esiste un numero reale \( M>0 \) tale che:
\( |x|>M \Rightarrow |f(x)-l|<\epsilon \),
ovvero se \( f(x) \) si avvicina arbitrariamente ad \( l \) a patto di prendere \( x \) sufficientemente grande.
In tale caso la retta \( y=l \) è un asintoto orizzontale per la funzione.
Esempio. Dato il limite:
\( \displaystyle \lim_{x \to +\infty}{e^{-x}+2}=2 \)
Si può vedere dalla figura:
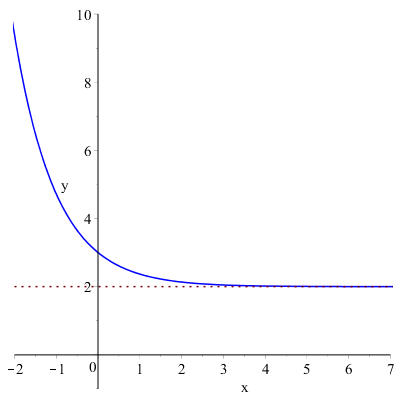
che più i valori della variabile \( x \) aumentano (tendendo a infinito), più i valori della variabile \( y \) si avvicinano al valore \( 2 \), ovvero la funzione si avvicina alla retta \( y=2 \) che rappresenta un asintoto orizzontale.
1.4. Definizione limite infinito all'infinito
Definizione. Si dice che la funzione \( y=f(x) \) tende ad infinito per \( x \) tendente all'infinito e si scrive\( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty\)
se per ogni \( M>0 \) esiste un \( k>0 \) tale che:
\( |x|>k \Rightarrow |f(x)|>M \),
ovvero se \( f(x) \) si avvicina arbitrariamente a \( \infty \) a patto di prendere \( x \) sufficientemente grande.
Esempio. Dato il limite:
\( \displaystyle \lim_{x \to +\infty}{ln(x)}=+\infty \)

Dalla figura si osserva che scelto un valore \( M \) arbitrariamente grande sull'asse \( y \) viene individuato in corrispondenza di esso un valore \( k \) sull'asse \( x \): i punti della funzione che superano questo valore \( M \) hanno le ascisse maggiori di \( k \).
2. Limite destro e sinistro
Si dice che la funzione \(y=f(x) \), per \( x \) tendente ad \( a \) da sinistra (o da destra), ha il limite sinistro (o destro) e si scrive
\( \displaystyle \lim_{x \to a^-}{f(x)}=l \) \( \displaystyle \left ( \lim_{x \to a^+}{f(x)}=l \right ) \)
se per ogni intorno di \( l \) di raggio \( \epsilon \) esiste un intorno sinistro (o destro) di \( a \) di raggio \( \delta \) tale che, comunque scelto nell'intorno di \( a \) un valore \( x \) appartenente al dominio e diverso da \(a \), il corrispondente valore \( f(x) \) cade nell'intorno di \( l \); ovvero, \( f(x) \) si avvicina arbitrariamente a \( l \) a patto di prendere \( x \) sufficientemente vicino ad \( a \) da sinistra (o da destra).
Se una funzione ha in un punto un limite finito, allora in quel punto il limite destro e il limite sinistro coincidono. Può accadere tuttavia che, in un punto, una funzione abbia soltanto il limite sinistro (oppure solo il destro), oppure che il limite sinistro e quello destro esistano entrambi, ma non coincidano.
Ad esempio, se consideriamo il grafico della funzione:
\( \displaystyle f(x)= \begin{cases}
1 \quad x \geq 0 \\
-1 \quad x<0
\end{cases} \)
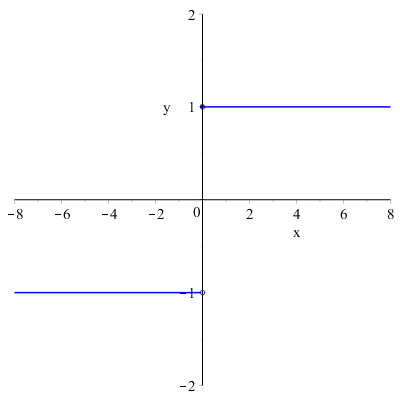
Si può notare che, quando la \( x \) si avvicina a \( 1 \) da destra, la funzione tende al valore \( y=1 \), mentre quando la \( x \) si avvicina a \( 1 \) da sinistra la funzione tende al valore \( y=-1 \), ovvero:
\( \displaystyle \lim_{x \to 1^-}{f(x)}=-1 \) e \( \displaystyle \lim_{x \to 1^+}{f(x)}=1 \)
In tale caso la funzione non ha limite per \( x \) tendente a \( 1 \), dato che il limite sinistro e destro non coincidono.