Calcolo dei limiti
| Sito: | E-Learning PP&S |
| Corso: | Classe Quarta - 4AL4 - Liceo Internazionale Scienze Applicate 4 anni |
| Libro: | Calcolo dei limiti |
| Stampato da: | Utente ospite |
| Data: | Friday, 22 November 2024, 03:20 |
1. Proprietà dei limiti
Teorema (unicità del limite)
Una funzione \( y=f(x) \) non può avere due limiti diversi per \( x \) tendente ad \( a \), ovvero se esiste il \( \displaystyle \lim_{x \to a}{f(x)}=l \) tale limite è unico (dove i simboli \( l \) ed \( a \) possono indicare sia un numero reale sia \( \infty \)).
Teorema (permanenza del segno)
Se una funzione ha limite non nullo per \( x \) tendente ad \( a \), allora in un intorno di \( a \) la funzione ha lo stesso segno del limite.
Teorema (del confronto)
In un intorno di \( a \), al più escluso \( a \), sono definite le funzioni \( h(x) \), \( g(x) \) e \( f(x) \) e vale \( h ( x ) \leq f ( x ) \leq g ( x ) \).
Si ha che se \( h ( x ) \) e \( g ( x ) \) tendono ad un limite finito \( l \) per \( x \) tendente a \( a \) allora anche \( \displaystyle \lim_{x \to a}{f(x)}=l \).
Operazioni con limiti finiti
Se esistono, finiti, i limiti
\( \displaystyle \lim_{x \to a}{f(x)}=l \) e \( \displaystyle \lim_{x \to a}{g(x)}=m \)
con \( l, m \in \mathbb{R} \), allora:
- \( \displaystyle \lim_{x \to a}{\left (f(x) \pm g(x) \right )}=l \pm m\)
- \( \displaystyle \lim_{x \to a}{-f(x)}=-l \)
- \( \displaystyle \lim_{x \to a}{\left (f(x) \cdot g(x) \right )}=l \cdot m\)
- \( \displaystyle \lim_{x \to a}{\left (\frac{f(x)}{g(x)} \right )}=\frac{l}{m}
\)
- \( \displaystyle \lim_{x \to a}{(k \cdot f(x))}=k \cdot l \) con \( k \in \mathbb{R} \)
1.1. Operazioni con limiti infiniti e forme indeterminate
Operazioni con limiti infiniti
- Se esiste il \( \displaystyle \lim_{x \to a}{f(x)}=\infty \), allora esiste il \( \displaystyle \lim_{x \to a}{\dfrac{1}{f(x)}}=0\).
\( f \) infinito \( \Rightarrow \) \( \dfrac{1}{f(x)} \) infinitesimo
- Se \( y=f(x) \) e \( y=g(x) \) tendono entrambe a \( +\infty \) o \( -\infty \), per \( x \) tendente ad \( a \), anche la funzione \( y=f(x)+g(x) \) tende rispettivamente a \( +\infty \) o \( -\infty \).
NOTA BENE: Il teorema non dice nulla nel caso in cui le due funzioni tendano ad infinito ma con segno diverso: in questo caso si ottiene un situazione indeterminata.
Per le operazioni con limiti infiniti si ottengono le seguenti forme indeterminate:
| \( \infty - \infty \) | \( 0 \cdot \infty \) | \( \dfrac{0}{0} \) | \( \dfrac{\infty}{\infty} \) |
|---|
Ottenere una forma indeterminata non significa che il limite non esiste, ma solo che il limite non è determinabile con le regole operative stabilite dai teoremi.
Esempio. Determinare:
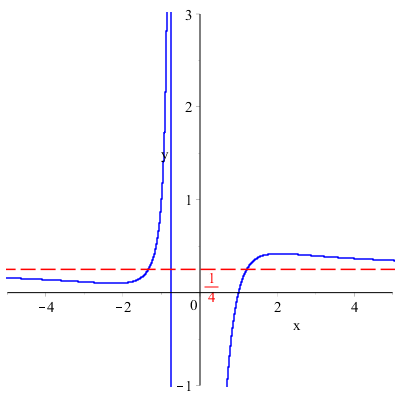
\( \displaystyle \lim_{x \to \infty}\dfrac{x^3+2x^2-3}{4x^3-x+1}=\infty \)
Sostituendo il valore \( \infty \) alla variabile \( x \) otteniamo la forma indeterminata \( \dfrac{\infty}{\infty} \).
Allora riscriviamo la funzione ponendo in evidenza \( x^3 \) al numeratore e al denominatore
e semplificando:\( \displaystyle \lim_{x \to \infty}\dfrac{x^3 \left (1+\dfrac{2}{x}-\dfrac{3}{x^3} \right )}{x^3 \left (4-\dfrac{1}{x^2}+\dfrac{1}{x^3} \right )}=\dfrac{1}{4} \)
Infatti quando \( x \) tende ad infinito, i termini che contengono una potenza di \( x \) al denominatore tendono a zero.
Graficamente questo risultato significa che la funzione ha un asintoto orizzontale di equazione \( y=\dfrac{1}{4} \).
1.2. Infinitesimi e infiniti
Può capitare di dover calcolare un limite che presenta la forma indeterminata \( \dfrac{0}{0} \), senza che sia possibile semplificare la funzione fratta. Si può allora giungere ad un risultato confrontando gli infinitesimi, cioè controllando quale fra la funzione che sta al numeratore e la funzione che sta al denominatore tende a zero più rapidamente.
Per questo scopo può aiutare il confronto fra grafici:
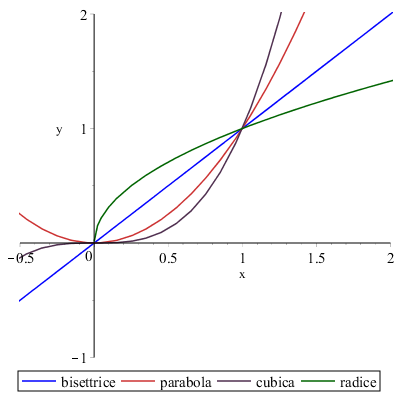
Se consideriamo il comportamento nell'intorno di zero delle funzioni disegnate vediamo che l'ordine con cui si avvicinano più velocemente allo zero è:
- cubica
- parabola
- bisettrice
- radice
Ciò significa che dalla cubica alla radice l'ordine di infinitesimo decresce. Di seguito alcuni esempi di limiti, che coinvolgono queste funzioni, la cui forma indeterminata è \( \dfrac{0}{0} \):
\( \displaystyle \lim_{x \to 0^+}{\dfrac{\sqrt{x}}{x^2}}=\infty \); \( \displaystyle \lim_{x \to 0^+}{\dfrac{x^3}{\sqrt{x}}}=0 \); \( \displaystyle \lim_{x \to 0^+}{\dfrac{x^3}{x^2}}=0 \)
Allo stesso modo può capitare di dover calcolare un limite che presenta la forma indeterminata \( \dfrac{\infty}{\infty} \), senza che sia possibile semplificare la funzione fratta. Si può allora giungere ad un risultato confrontando gli infiniti, cioè controllando quale fra la funzione che sta al numeratore e la funzione che sta al denominatore tende a infinito più rapidamente.
Per questo scopo può aiutare il confronto fra grafici:
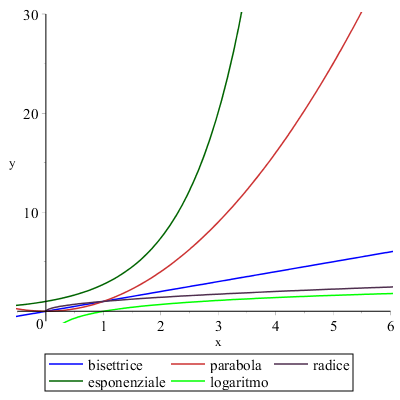
Se consideriamo il comportamento nell'intorno di \( +\infty \) delle funzioni disegnate vediamo che l'ordine con cui si avvicinano più velocemente a \( +\infty \) è:
- esponenziale
- parabola
- bisettrice
- radice
- logaritmo
Ciò significa che dall'esponenziale al logaritmo l'ordine di infinito decresce. Di seguito alcuni esempi di limiti, che coinvolgono queste funzioni, la cui forma indeterminata è \( \dfrac{\infty}{\infty} \):
\( \displaystyle \lim_{x \to +\infty}{\dfrac{e^x}{\sqrt{x}}}=\infty \); \( \displaystyle \lim_{x \to +\infty}{\dfrac{\ln{x}}{x}}=0 \); \( \displaystyle \lim_{x \to +\infty}{\dfrac{x^2}{\ln{x}}}=\infty \);
1.3. Calcolo dei limiti
Poiché normalmente anche le funzioni più complesse sono il risultato della composizione di funzioni elementari, è indispensabile conoscere bene il valore dei limiti delle funzioni elementari agli estremi del loro dominio:
- funzione identità: \( f(x)=x \)
\( \displaystyle \lim_{x \to -\infty}{f(x)}=-\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione potenza con esponente pari: \( f(x)=x^n \) con \( n \) pari
\( \displaystyle \lim_{x \to -\infty}{f(x)}=+\infty\); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione potenza con esponente dispari: \( f(x)=x^n \) con \( n \) dispari
\( \displaystyle \lim_{x \to -\infty}{f(x)}=-\infty\); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \)
- funzione esponenziale con base maggiore di 1: \( f(x)=a^x \) con \( a>1 \)
\( \displaystyle \lim_{x \to -\infty}{f(x)}=0 \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione esponenziale con base minore di 1: \( f(x)=a^x \) con \(0< a<1 \)
\( \displaystyle \lim_{x \to -\infty}{f(x)}=+\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=0 \) - funzione logaritmica con base maggiore di 1: \( f(x)=\log_a{x} \) con \( a>1 \)
\( \displaystyle \lim_{x \to 0^+}{f(x)}=-\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione logaritmica con base minore di 1: \( f(x)=\log_a{x} \) con \( 0<a<1 \)
\( \displaystyle \lim_{x \to 0^+}{f(x)}=+\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=-\infty \)
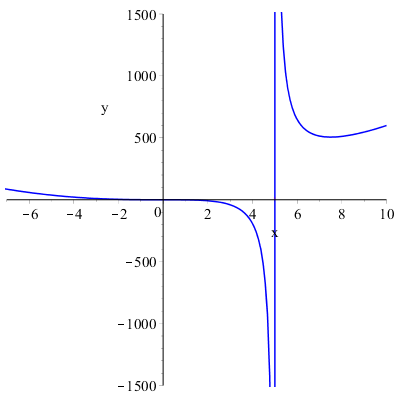
possiamo dedurre che:
\( \displaystyle \lim_{x \to -\infty}{f(x)}=+\infty \)
\( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \)
\( \displaystyle \lim_{x \to 5^-}{f(x)}=-\infty \)
\( \displaystyle \lim_{x \to 5^+}{f(x)}=+\infty \)
la retta \(x=5\) è un asintoto verticale.
1.4. Alcuni limiti notevoli
Vi sono alcuni limiti, detti limiti notevoli, che sono molto utili nella risoluzione delle varie forme indeterminate; i principali sono i seguenti:
\( \displaystyle \lim_{x \to 0} \dfrac{\sin x}{x}=1 \)
\( \displaystyle \lim_{x \to 0} \dfrac{1-\cos x}{x^2}=\dfrac{1}{2} \)
\( \displaystyle \lim_{x \to 0} \dfrac{e^x-1}{x}=1 \)
\( \displaystyle \lim_{x \to 0} \dfrac{\ln(1+x)}{x}=1 \)
\( \displaystyle \lim_{x \to \pm \infty} \bigr(1+\dfrac{1}{x}\Bigl)^x=e \)
Esempio: Calcoliamo \( \displaystyle \lim_{x \to 0}{\dfrac{1-\cos{x}}{\sin{4x}}} \)
Riscriviamo il limite nel seguente modo:
\( \displaystyle \lim_{x \to 0}{(1-\cos{x}) \cdot \dfrac{1}{\sin{4x}}}=\lim_{x \to 0}{x^2 \cdot \dfrac{1-\cos{x}}{x^2} \cdot \dfrac{1}{4x} \cdot \dfrac{4x}{\sin{4x}}} = 0\)
Dal momento che:
\( \displaystyle \lim_{x \to 0} \dfrac{\sin 4x}{4x}=1 \) e \( \displaystyle \lim_{x \to 0} \dfrac{1-\cos x}{x^2}=\dfrac{1}{2} \)