Continuità di una funzione
| Sito: | E-Learning PP&S |
| Corso: | Classe Quarta - 4AL4 - Liceo Internazionale Scienze Applicate 4 anni |
| Libro: | Continuità di una funzione |
| Stampato da: | Utente ospite |
| Data: | Sunday, 24 November 2024, 12:21 |
1. Le funzioni continue
Da un punto di vista intuitivo, una funzione è continua quando è possibile tracciare il suo grafico "senza staccare la penna dal foglio".
Utilizzando la definizione di limite, affermiamo che una funzione \(y=f(x) \) è continua in un punto \( a \in \mathbb{R} \) se vi è definita ed il suo limite, per \( x \) tendente ad \( a \), coincide con il valore della funzione in \( a \):
\( \displaystyle \lim_{x \to a}{f(x)}=f(a) \)
Una funzione si dice continua in un intervallo (o in tutto il suo insieme di definizione) se è continua in ogni suo punto.
NOTA BENE. Conoscere gli intervalli nei quali una funzione è continua è piuttosto importante, perché dove è continua non c'è necessità di calcolarne il limite: il calcolo del limite si effettua soltanto nei punti di discontinuità oppure per \( x \) tendente all'infinito.
Esempi di funzione continue
- La funzione costante \( y=k \) è continua in \( \mathbb{R} \)
- La funzione identica \( y=x \) è continua in \( \mathbb{R} \)
- Ogni funzione polinomiale è continua in \( \mathbb{R} \)
- Ogni funzione razionale fratta \( y=\dfrac{p(x)}{q(x)} \) è continua in \( \mathbb{R}-{x,q(x)=0} \)
- Le funzioni \( y=\cos{x} \) e \( y=\sin{x} \) sono continua in \( \mathbb{R} \)
- La funzione \( y=e^x \) è continua in \( \mathbb{R} \)
1.1. Punti di discontinuità
I casi di discontinuità di una funzione possono essere di diverso tipo:
- discontinuità di prima specie: se i suoi limiti sinistro e destro per x che tende a \(a\) esistono finiti ma sono diversi tra loro. Almeno uno dei due limiti risulta diverso da \( f(a) \) e si chiama salto della funzione in \( a \) il valore assoluto della differenza dei due limiti.
Esempio: La funzione \( f(x)= \begin{cases} 1 \quad x \geq 0\\ -1 \quad x<0 \end{cases} \)
presenta una discontinuità di prima specie nel punto \( x=0 \) poiché: \( \displaystyle \lim_{x \to 0^-} f(x)=-1 \) e \( \displaystyle \lim_{x \to 0^+} f(x)=1 \). Il salto è pari a 2.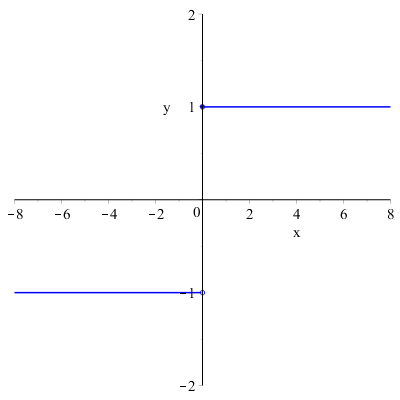
discontinuità di seconda specie: se per x che tende ad \(a\) almeno uno dei suoi limiti sinistro e destro o non esiste o vale \( \pm \infty \).
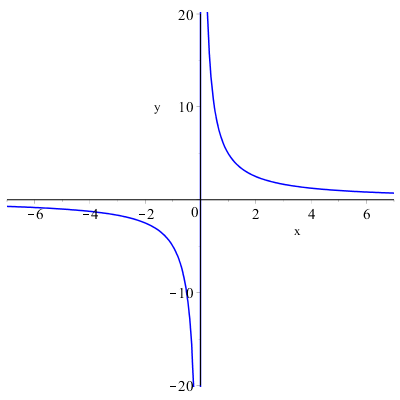
Esempio: La funzione \( y=\dfrac{1}{x} \) presenta nel punto \( x=0 \) una discontinuità di seconda specie essendo:
\( \displaystyle \lim_{x \to 0^-} f(x)=-\infty \) e \( \displaystyle \lim_{x \to 0^+} f(x)=+\infty \).
- discontinuità di terza specie o eliminabile: se esiste finito il limite per x che tende a \(a\) (cioè i suoi limiti sinistro e destro esistono e sono uguali tra loro), ma tale limite non coincide con il valore della funzione in \(a\). Il termine eliminabile sta ad indicare che la funzione può essere facilmente resa continua in \(a\) modificando il suo valore in \(a\) e ponendo \( l=f(a) \) nel caso in cui \( a \) non sia nel dominio, oppure inserendo il punto \(a\) nel dominio.
Esempio: La funzione \( f(x)=\begin{cases} \ln{x} \quad x \neq 1\\ 2 \quad x=1 \end{cases} \)
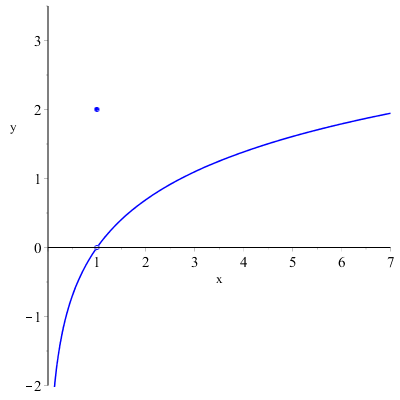
presenta nel punto \( x=1 \) una discontinuità di terza specie essendo: \( \displaystyle \lim_{x \to 1} f(x)=0 \), ma \( f(1)=2 \).