Le successioni
| Sito: | E-Learning PP&S |
| Corso: | Classe Quarta - 4AL4 - Liceo Internazionale Scienze Applicate 4 anni |
| Libro: | Le successioni |
| Stampato da: | Utente ospite |
| Data: | Saturday, 3 May 2025, 12:01 |
1. Le successioni numeriche
I numeri naturali, i numeri pari e dispari, i numeri primi sono esempi di successioni numeriche. Sono insiemi numerici infiniti, numerabili, linearmente ordinati e discreti (è possibile fornire un elenco dei loro elementi, indicando qual è il primo di essi e come si ottiene da un elemento il suo successivo). Ogni elemento o termine della successione è individuato dal posto che occupa nell'ordinamento: a0,a1,a2,...,an,....
Una successione è individuata dalla corrispondenza biunivoca, indicata con f, che associa ad ogni elemento di N il corrispondente elemento della successione. Per indicare una successione è sufficiente esprimere il suo termine generico an.
Esempio. Qual è la successione individuata dalla funzione f(n)=2−n?
Costruiamo i primi termini della successione:
0→20=1
1→2−1=12
2→2−2=14
I termini della successione sono:
1,12,14,18,116,...,12n
Se rappresentatiamo graficamente la successione otteniamo:
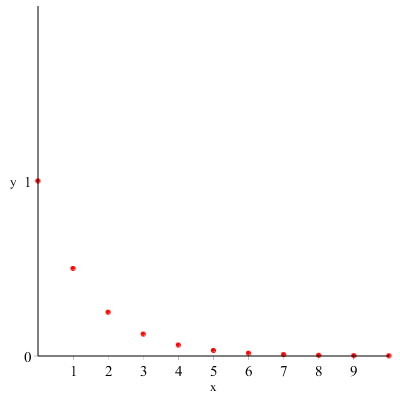
Si può definire una successione:
- per definizione del termine generale, dando la legge che associa al numero naturale n il corrispondente elemento an (come nell'esempio precedente)
- per ricorrenza, ovvero quando il termine generale è espresso in funzione di uno o più termini precedenti; in tal caso la successione può essere calcolata solo quando sono noti i termini iniziali. Ad esempio, la successione definita dalla relazione:
an+1=a2n+1 con a0=1
esprime la successione i cui primi elementi sono: 1,2,5,26,....
Infatti:
a2=a21+1=1+1=2
a3=a22+1=4+1=5
a4=a23+1=25+1=26..
1.1. Proprietà e limiti delle successioni
Dato che le successioni sono definite da funzioni, è possibile calcolarne il limite per studiarne l'andamento al crescere di \(n \), ovvero \( \displaystyle \lim_{n \to +\infty} a_n \).
Una successione può essere
- convergente: se esiste finito il \( \displaystyle \lim_{n \to +\infty} a_n \).
Ad esempio, \(a_n=2-\dfrac{1}{n^2} \)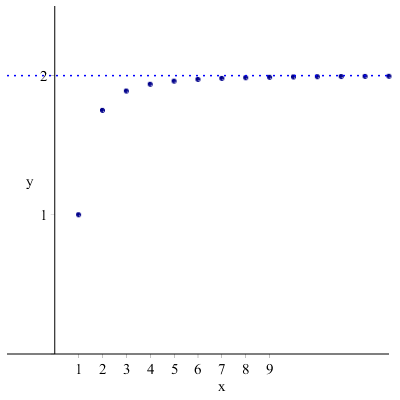
- divergente: se esiste infinito il \( \displaystyle \lim_{n \to +\infty} a_n \).
Ad esempio, \(a_n=3n^3 \)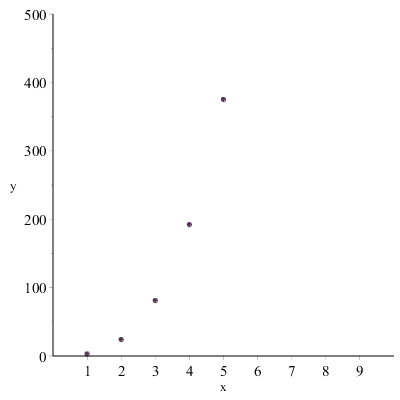
- irregolare: se il limite non esiste.
Ad esempio, \(a_n=\sin{\dfrac{n\pi}{2}}\)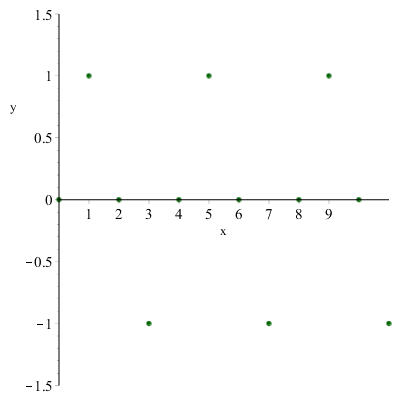
Non bisogna confondere la caratteristica di una successione di essere convergente o divergente con quella di essere crescente o decrescente. Quest'ultime indicano solo che i termini sono via via rispettivamente più grandi (per ogni \(n\), \(a_n>a_{n-1} \)) o più piccoli (per ogni \(n\), \(a_n<a_{n-1}\)), e indicano la possibilità che la successione sia limitata.
NOTA BENE. Una successione può essere crescente senza essere divergente, e una successione decrescente può essere divergente.
Esempio: Determiniamo il carattere della successione \( a_n=1 + \frac{1}{3n} \) attraverso il calcolo del limite:
\( \displaystyle \lim_{n \to +\infty} \left( 1 + \frac{1}{3n} \right)^{2n}=\Bigr[ \displaystyle \lim_{n \to +\infty} \left( 1 + \frac{1}{3n} \right)^{3n} \Bigl]^{\frac{2}{3}}=e^{\frac{2}{3}}=\sqrt[3]{e^2} \)
si tratta di una successione regolare convergente.
Esempio: Determiniamo il carattere della successione \( \dfrac{n^{6} + \ln{n} + 3^{n}}{2^{n} + n^{4} + \ln^{5}{n}} \):
\( \displaystyle \lim_{n \to +\infty} \frac{n^{6} + \ln{n} + 3^{n}}{2^{n} + n^{4} + \ln^{5}{n}}=\displaystyle \lim_{n \to +\infty} \frac{3^{n}}{2^{n}}=+ \infty \)
Si tratta di una successione regolare divergente.
1.2. Le progressioni aritmetiche e geometriche
Due importanti esempi di successioni sono:
- La successione aritmetica è una successione ottenuta a partire da un primo termine \( a_0 \) addizionando ogni volta lo stesso numero, indicato con \(q\), detto ragione della successione.
Una successione aritmetica è definita dalla formula ricorsiva:\( a_n=a_0+n \cdot q \) con \( a_0, q \in \mathbb{R} \)
È detta "aritmetica" perché il termine n-esimo è la media aritmetica dei termini (n‒1)-esimo e (n+1)-esimo.
Esempio: la successione dei numeri dispari è una successione aritmetica di ragione 2. - La successione geometrica è una successione ottenuta a partire da un primo termine \( a_0 \) moltiplicando ogni volta per il numero stesso, indicato con \(q\), detto ragione della successione.
Una successione geometrica è definita dalla formula ricorsiva:\( a_n=a_0 \cdot q^{n} \) con \( a_0, q \in \mathbb{R} \)
È detta "geometrica" perché per \( q > 0 \) e \( a_0 > 0 \) il termine n-esimo è la media geometrica dei termini (n‒1)-esimo e (n+1)-esimo.
Esempio: le potenze di 3 sono una successione geometrica di ragione 3.