1.3 Scomposizione di polinomi
| Sito: | E-Learning PP&S |
| Corso: | Naretti Flavio - Istituti Secondari di Primo Grado - 3E |
| Libro: | 1.3 Scomposizione di polinomi |
| Stampato da: | Utente ospite |
| Data: | Friday, 2 May 2025, 19:57 |
1. Metodi di scomposizione
Scomporre un polinomio significa esprimerlo come prodotto di due o più fattori di grado inferiore, che possono essere monomi o polinomi in parentesi.
Per farlo, è possibile utilizzare dei metodi noti, che verranno riportati nei prossimi paragrafi!
1.1. Raccoglimento a fattore comune
Il metodo di raccoglimento a fattore comune consiste nel mettere in evidenza il più grande fattore comune a tutti i termini del polinomio, ossia il loro massimo comune denominatore (MCD).Poniamo il MCD fuori dalla parentesi, all'interno della quale scriviamo il nostro polinomio, dopo aver diviso ogni suo termine per il massimo comune divisore.
Esempio: 6ab−9ac+3ad=3a⋅(2b−3c+d)
1.2. Scomposizione utilizzando i prodotti notevoli
Differenza di due quadrati
Sapendo che il prodotto della somma di due termini per la loro differenza è uguale alla differenza tra i loro quadrati, dall'espressione \( a^2 - b^2\) si può risalire ai due fattori \( (a + b) \) e \( (a - b) \).
Pertanto, se un binomio è una differenza di due quadrati, esso può essere scomposto nel seguente modo:
\( a^2 - b^2 = (a + b) \cdot (a - b) \)
Esempio: \( 9 x^2 - 5 y^4 = (3 x + \sqrt{5} y^2) \cdot (3 x - \sqrt{5} y^2) \)
Quadrato di un binomio
Se l'espressione letterale consiste in un trinomio, di cui due termini sono quadrati di monomi e il terzo termine è il doppio del prodotto dei due monomi, essa può essere scomposta come quadrato di un binomio:
\( a^2 - 2 a b + b^2 = (a - b)^2 \)
\( a^2 + 2 a b + b^2 = (a + b)^2 \)
Esempi: \( 9 x^2 + 7 z^6 - 6 \sqrt{7} x z^3 = (3 x - \sqrt{7} z^3)^2 \)
\( 9 x^2 + 7 z^6 + 6 \sqrt{7} x z^3 = (3 x + \sqrt{7} z^3)^2 \)
Cubo di un binomio
Un quadrinomio (ossia un polinomio di quattro termini) è un cubo di un binomio, se si presenta nella seguente forma:
\( a^3 - 3 a^2 b + 3 a b^2 - b^3 = (a - b)^3\)
Esempio: \( x^3 - 9 x^2 y^2 + 27 x y^4 - 27 y^6 = ( x - 3 y^2)^3 \)
1.3. Regola di Ruffini
Un polinomio di grado n a coefficienti reali nella sola variabile x, che indichiamo con P(x), può essere scritto ordinatamente, secondo le potenze decrescenti di x:
\( P(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + ... + a_1 x + a_0\)
con \( n \in \mathbb{N}\) e \(a_0,...,a_n \in \mathbb{R} \).
Il teorema di Ruffini stabilisce che il valore che il polinomio P(x) assume sostituendo a x il numero \(r \in \mathbb{R}\) è uguale al resto della divisione di P(x) per il binomio \(A(x) = x - r\).
Il polinomio P(x) è quindi divisibile per il binomio \(A(x)\) se e solo se \(r\) è uno zero di P(x), cioè se e solo se \( P(r) = 0\).
Dividendo P(x) per A(x), si ottiene il polinomio quoziente
\( Q(x) = b_{n-1} x^{n-1} + b_{n-2} x^{n-2} +... + b_1 x +b_0\)
La divisione polinomiale può essere eseguita con il seguente algoritmo, noto come "regola di Ruffini":
- i coefficienti di P(x) vengono scritti tra le due linee verticali e il termine noto a destra di esse;
- si riporta sotto la linea il primo coefficiente;
- si moltiplica il coefficiente scritto (\( a_n\)) per \(r\) e si scrive il risultato nella colonna successiva, sotto il secondo termine (\( a_{n-1}\));
- si esegue l'addizione in colonna e si individua così un nuovo coefficiente;
- si ripete l'operazione per ogni coefficiente.
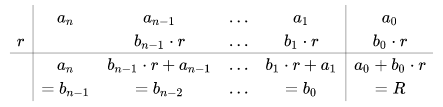
I coefficienti \( b_{n-1},...,b_0\) sono i coefficienti del polinomio quoziente Q(x), mentre R è il resto della divisione, che è nullo se r è uno zero del polinomio.