2.2 Risolvere un'equazione
| Sito: | E-Learning PP&S |
| Corso: | Naretti Flavio - Istituti Secondari di Primo Grado - 3E |
| Libro: | 2.2 Risolvere un'equazione |
| Stampato da: | Utente ospite |
| Data: | Monday, 7 April 2025, 00:54 |
Descrizione
In questo libro si spiega come risolvere equazioni di primo grado
2.1 Principi di equivalenza
Due equazioni si dicono equivalenti se hanno le stesse soluzioni.
Ad esempio le equazioni:
\( 2 \cdot x+1 = 3 \cdot x -4 \quad \quad \text{e} \quad \quad 4-x=5 \cdot x -26 \)
ammettono come unica soluzione \( x=5 \), infatti sostituendo la \(x \) con il numero \( 5 \) :
\( 2 \cdot 5+1 = 3 \cdot 5 -4 \quad \quad \text{e} \quad \quad 4-5=5 \cdot 5 -26 \)
cioè
\( 11 = 11 \quad \quad \text{e} \quad \quad-1=-1 \)
si ottengono due identità.
Primo principio di equivalenza
Addizionando o sottraendo ai due membri di un'equazione uno stesso numero o una stessa espressione algebrica contenente l'incognita si ottiene un'equazione equivalente a quella di partenza.
Esempio
Data l'equazione
\( 2 \cdot x -1 = 4 \cdot x +5 \)
la cui soluzione è \( x=-3 \), infatti
\( 2 \cdot (-3) -1 = 4 \cdot (-3) +5 \quad \text{ cioè } \quad -7 = -7 \)
possiamo aggiungere ad entrambi i membri il numero \( +1 \) , ottenendo così l'equazione
\( 2 \cdot x -1 +1 = 4 \cdot x +5 +1 \)
Cioè
\( 2 \cdot x = 4 \cdot x +6 \)
che è risolta dalla stessa soluzione \( x=-3 \).
In pratica in questo esempio abbiamo eliminato il termine -1 dal primo membro e lo abbiamo spostato nel secondo membro, cambiato di segno. Dal primo principio di equivalenza segue la regola pratica (legge del trasporto):
In ogni equazione un termine qualsiasi può essere spostato da un membro all'altro purchè lo si cambi di segno.
Secondo principio di equivalenza
Moltiplicando o dividendo entrambi i membri di un'equazione uno stesso numero diverso da zero si ottiene un'equazione equivalente a quella di partenza.
Esempio
Data l'equazione
\( 2 \cdot x -4 = 4 \cdot x +6 \)
la cui soluzione è \( x=-5 \), infatti
\( 2 \cdot (-5) -4 = 4 \cdot (-5) +6 \quad \text{ cioè } \quad -14 = -14 \)
possiamo dividere entrambi i membri per \( +2 \) , ottenendo così l'equazione
\( \frac{2 \cdot x -4}{2} = \frac{4 \cdot x +6}{2} \)
Cioè
\( x - 2 = 2 \cdot x +3 \)
che è risolta dalla stessa soluzione \( x=-5 \).
2.2 Risoluzione di un'equazione di primo grado
Consideriamo equazioni di primo grado in un'incognita. Risolvere questo tipo di equazioni significa trovare quei valori che, sostituiti all'incognita \(x \) rendono l'equazione un'identità.Per risolvere un'equazione si possono utilizzare i principi di equivalenza per trasformarla in un'equazione equivalente nella forma \( x = k \) dove \( k \) è un numero: tale numero è la soluzione dell'equazione.
Il procedimento che in genere si segue è il seguente
| \( x-4=6+3x \) |
|
|---|---|
| 1. Si separano i termini contenenti l'incognita dai termini noti utilizzando la regola del trasporto: si spostano tutti i termini con l'incognita al primo membro e tutti i termini noti al secondo membro |
\( x-3x = 4+6 \) |
| 2. Si eseguono le somme in modo da scrivere l'equazione nella forma \( a \cdot x = b \) |
\( -2x = 10 \) |
| 3. Se \(a \) è diverso da \( 0 \) si applica il secondo principio di equivalenza dividendo entrambi i membri per \( a \), il coefficiente della \( x \) a primo membro. |
\( \frac{-2x}{-2} = \frac{10}{-2} \) |
| 4. Si ottiene un'equazione equivalente scritta nella forma: \( x = \frac{b}{a} \) . Questa è la soluzione (unica) dell'equazione. |
\( x = -5 \) |
| 5. Si esegue la verifica sostituendo la soluzione trovata nell'equazione di partenza e controllando che si tratti di un'identità. | \( -5-4=6+3 \cdot (-5) \quad \\ \text{cioè} \quad -15 = -15 \) |
2.3 Equazioni determinate, indeterminate, impossibili
Risolvendo un'equazione, dopo aver spostato i termini contenenti l'incognita al primo membro e i termini noti al secondo membro, si ottiene un'equazione nella forma \( ax=b \). Qui è necessario fermarsi e studiare l'equazione trovata. In particolare:- Se \( a \neq0 \) l'equazione si può risolvere e ammette un'unica soluzione \( x = \frac{b}{a} \). L'equazione si dice determinata.
- Se \( a = 0 \) non si può applicare il secondo principio di equivalenza in quanto non è possibile dividere per zero i due membri dell'equazione. Si possono distinguere due casi:
- Se \( b \neq0 \) l'equazione, che risulta scritta nella forma \( 0 = b \) è impossibile.
- Se \( b = 0 \) l'equazione equivale all'identità \( 0 = 0 \), ammette come soluzione qualsiasi numero: si dice indeterminata.
2.4 Risoluzione grafica di un'equazione
Consideriamo un'equazione di primo grado in un'incognita, ad esempio:
\( 3x-5 = 7-x \)
Considerando separatamente i due membri, ciascuno di essi può essere descritto come funzione di \( x \), cioè le due espressioni \( 3x-5 \) e \( 7-x \) assumono valori diversi quando si sostituisce un diverso numero alla \(x \). In particolare entrambe possono essere rappresentate graficamente come due rette:
\( y = 3x-5 \quad \text{e} \quad y = 7-x \)
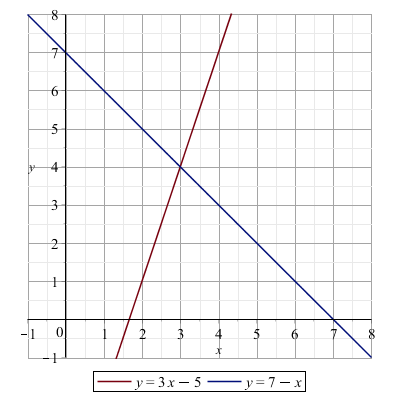
La soluzione dell'equazione è il valore di \( x \) per cui le due rette si incontrano.
In questo caso la soluzione dell'equazione è \( x=3 \) . Quando si sostituisce tale valore nell'equazione si ottiene l'identità \( 4=4 \), che corrisponde all'ordinata del punto di intersezione delle due rette.
Equazioni determinate, indeterminate, impossibili
Come abbiamo visto prima, ogni equazione di primo grado in un'incognita può essere interpretata graficamente come una coppia di rette; la soluzione dell'equazione corrisponde all'intersezione. In particolare:Un'equazione determinata ammette una e una sola soluzione, e corrisponde ad una coppia di rette incidenti, che si incontrano in un unico punto.
Ad esempio, l'equazione \( 2x-5=-3x \), che ha soluzione \( x=1 \) può essere rappresentata come la coppia di rette
\( y = 2x-5 \)
\( y = -3x+1 \)
che si intersecano nel punto \( (1,-3) \)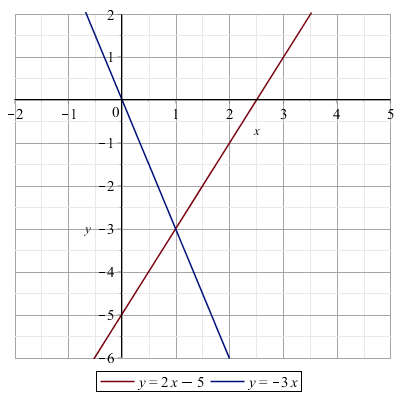
- Un'equazione indeterminata ammette infinite soluzioni (tutti i numeri reali) e corrisponde ad una coppia di rette coincidenti (si incontrano in tutti i loro punti).
Ad esempio, l'equazione \( 3x-1=3(x+1)-4 \), la cui soluzione è indeterminata, può essere rappresentata come la coppia di rette
\( y = 3x-1 \)
\( y = 3(x+1)-4 \)
che sono coincidenti.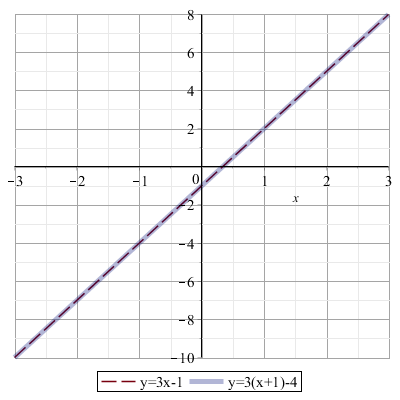
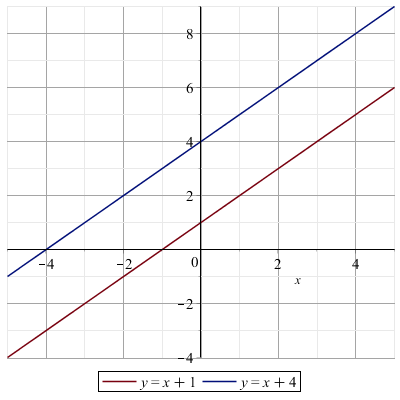
- Un'equazione impossibile corrisponde ad una coppia di rette parallele: non si incontrano mai.
Ad esempio, l'equazione \( x+1=x+3 \), che è impossibile, può essere rappresentata come la coppia di rette
\( y = x+1 \)
\( y = x+3 \)
che sono parallele.