3.1 Le funzioni

Sito:	E-Learning PP&S
Corso:	Naretti Flavio - Istituti Secondari di Primo Grado - 3E
Libro:	3.1 Le funzioni

Stampato da:	Utente ospite
Data:	sabato, 27 aprile 2024, 14:00

Sommario

1.1 Variabili e costanti
1.2 Le funzioni
1.3 Tabelle e grafici

1.1 Variabili e costanti

Introduciamo le variabili analizzando un problema:

"Tre amici vanno ad uno spettacolo teatrale.
In base alla posizione a sedere, vi sono tre tipi di biglietto: da 10€, da 15€ e da 20€.

Inoltre, una volta arrivati decidono di comprare una bibita a testa, del costo di 2€.

Considerando che gli amici decidono di comprare tutti lo stesso tipo di biglietto, in modo da sedersi vicini, quanto pagheranno in tutto?"

Inseriamo l'incognita y che indicherà la spesa totale dei tre amici:

\( y= spesa \) .

Se gli amici decidono di comprare il biglietto da 10€ la loro spesa y sarà data da:
\( y=3 \cdot10+3 \cdot 2 = 30 + 6 = 36 \) .
Se gli amici decidono di comprare il biglietto da 15€ la loro spesa y sarà data da:
\( y=3 \cdot15+3 \cdot 2 = 45 + 6 = 51 \) .
Se gli amici decidono di comprare il biglietto da 20€ la loro spesa y sarà data da:
\( y=3 \cdot20+3 \cdot 2 = 60 + 6 = 66 \) .

Riassumendo:


Prezzo di un biglietto in €	Costo di tre biglietti in €	Costo di tre bibite in €	Spesa totale y
10	30	6	36
15	45	6	51
20	60	6	66

Se confrontiamo quindi la spesa totale per ciascun tipo di biglietto, ci rendiamo conto che ogni calcolo è molto simile al precedente, con la sola eccezione del prezzo di ingresso che è VARIABILE.
I numeri 10, 15, 20 indicano i diversi prezzi del biglietto di ingresso; la spesa totale y è stata espressa nei seguenti modi:


Prezzo di un biglietto in €	Spesa totale y
10	\( y=3 \cdot10+3 \cdot 2 = 36 \)
15	\( y=3 \cdot15+3 \cdot 2 = 51 \)
20	\( y=3 \cdot20+3 \cdot 2 = 66 \)

In generale potremmo quindi indicare il prezzo di un biglietto con un simbolo qualsiasi, per esempio la lettera x e scrivere la spesa totale nel seguente modo:

\( y=3 \cdot x+3 \cdot 2 \) con \( x \in \) {10, 15, 20}.

Definiamo quindi:

x variabile indipendente, della quale è sempre necessario sapere che valori può assumere, cioè è necessario sapere l'insieme degli elementi al quale appartiene (per es. l'insieme dei costi dei biglietti {10, 15, 20}).
y variabile dipendente, in quanto il suo valore dipende dal valore assunto da x.

Inoltre, nel nostro esempio abbiamo:

una grandezza variabile indipendente, ovvero il prezzo del biglietto;
una grandezza variabile dipendente, ovvero la spesa totale che dipende dal prezzo del biglietto;
una grandezza costante, ovvero il costo della bibita, che è sempre fissa.

Definiamo quindi:

grandezze variabili quelle che possono assumere più di un valore;
grandezze costanti quelle che conservano sempre lo stesso valore.

1.2 Le funzioni

Quando una grandezza dipende da un'altra grandezza variabile in modo che ad ogni valore di quest'ultima corrisponde un solo valore per la prima grandezza, questa si dice funzione della seconda.

La variabile dipendente e la variabile indipendente sono una funzione dell'altra.

Per es.
la spesa totale dei tre amici andando a teatro è funzione del prezzo del biglietto.
Questa si può esprimere tramite una formula matematica:

\( y=3 \cdot x+6 \) .

Questo tipo di relazione, espressa tramite una formula matematica, tra la variabile x indipendente e la variabile y dipendente, si chiama funzione matematica e si scrive

y=f(x).

Con questo si intende dire che la variabile y è funzione (ovvero dipende) dalla variabile x.

1.3 Tabelle e grafici

Per esaminare la relazione che intercorre tra due grandezze variabili, si può ricorrere all'esame di una tabella nella quale sono riportati i valori assunti dalle variabili, oppure si può più semplicemente ricorrere ad un grafico che mostra immediatamente il tipo di relazione che intercorre tra le due variabili e che è più facile a leggersi e più conciso.

Tornando all'esempio del paragrafo 1.2, esprimiamo la spesa totale y dei tre amici in funzione del prezzo x del biglietto tramite la formula \( y=3 \cdot x+6 \) .

Per rappresentarla possiamo utilizzare una tabella:


Variabile indipendente x	Variabile dipendente y
10	\( y=3 \cdot 10+6 =36 \)
15	\( y=3 \cdot 15+6 =51 \)
20	\( y=3 \cdot 20+6 =66 \)

In alternativa, possiamo utilizzare un grafico per rappresentare la funzione \( y=3 \cdot x+6 \) :

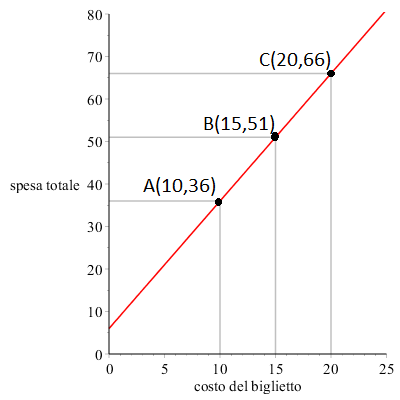
Per tracciarlo abbiamo disegnato i punti A, B, C calcolati precedentemente e li abbiamo quindi congiunti con una retta.
Sapevamo già a priori che il grafico sarebbe stato una retta in quanto la formula matematica che lega le nostre variabili è una funzione lineare (ovvero di primo grado).