4.1 Statistica
| Sito: | E-Learning PP&S |
| Corso: | Naretti Flavio - Istituti Secondari di Primo Grado - 3E |
| Libro: | 4.1 Statistica |
| Stampato da: | Utente ospite |
| Data: | domenica, 13 aprile 2025, 11:52 |
1.1 Che cos'è la statistica
Tutti i giorni sentiamo espressioni come "Statisticamente parlando..", "I dati statistici rivelano che..", e i giornali pubblicano dati statistici espressi in cifre su svariati campi delle attività umane: industria, agricoltura, scuola, amministrazione pubblica, sport, prezzi, popolazione, ecc..
Per capire cos'è la statistica facciamo un esempio: si voglia fare un'indagine sullo sport preferito dai ragazzi che frequentano il primo anno delle scuole superiori di una certa provincia. Per far ciò si sceglie un piccolo numero (rispetto al totale) dei ragazzi che frequentano il primo anno delle scuole superiori, per esempio quelli della propria scuola che diventa la scuola campione.
Si potrà poi dedurre che quello che è vero per la vostra scuola è vero in tutta la vostra provincia. I risultati ottenuti si possono raccogliere in una tabella come la seguente:
| Sport preferito | Numero di preferenze | Percentuale |
|---|---|---|
| CALCIO | 24 | 2450=48% |
| PALLAVVOLO | 7 | 750=14% |
| TENNIS | 2 | 250=4% |
| ATLETICA LEGGERA | 6 | 650=12% |
| ALTRI SPORT | 11 | 1150=22% |
| Totale allievi intervistati | 50 | 100% |
Statisticamente si ha che i ragazzi del primo anno delle scuole superiori preferiscono come sport il gioco del calcio per il 48%.
Un'indagine come la precedente si chiama campionamento: esso si usa nei sondaggi d'opinione pubblica, per controllare la qualità dei prodotti di un'industria, per avere informazioni sul decorso di una certa malattia infettiva, etc.
I metodi statistici (tabelle, diagrammi, ..) ci aiutano a leggere e interpretare i dati e ci permettono di fare previsioni. Si può dire che <<la statistica è l'arte di interpretare i dati>>.
1.2 Indagine statistica
Una corretta indagine statistica procede attraverso 3 fasi:
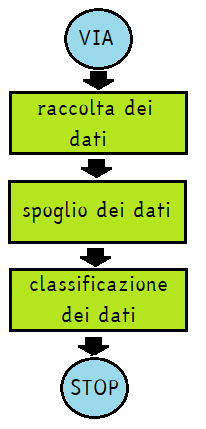
Il primo passo nel'applicazione dei metodi statistici è raccogliere bene i dati.
- Poiché un'indagine statistica sia ben fatta i dati raccolti devono essere appropriati e inerenti all'indagine.
- Una volta deciso quali dati raccogliere di devono distinguere i dati primari (raccolti direttamente dalle persone coinvolte nel problema) e i dati secondari (raccolti attraverso pubblicazioni, registrazioni, etc.).
Una volta che i dati sono stati raccolti, per ricavarne delle informazioni è necessario procedere allo spoglio dei dati, ovvero riorganizzarli in un ordine diverso da quello ottenuto durante la raccolta e infine alla classificazione dei dati in tabelle.
Esempio
Da un'indagine svolta in una classe sull'altezza degli allievi si sono ottenuti i seguenti dati in (cm)
| 152 | 155 | 161 | 171 | 158 | 148 | 149 | 168 | 140 | 144 |
|---|---|---|---|---|---|---|---|---|---|
| 170 | 142 | 150 | 153 | 153 | 142 | 156 | 151 | 165 | 168 |
- da \( 140 \) a \( 150 \) cm
- da \( 150 \) a \( 160 \) cm
- da \( 160 \) a \( 170 \) cm
- da \( 170 \) a \( 180 \) cm
Infine è possibile ordinare e classificare i dati in una tabella (detta tabella di frequenza):
| Fascia d'altezza (cm) | Frequenza |
|---|---|
| \( 140 \)-\( 150 \) | 6 |
| \( 150 \)-\( 160 \) | 8 |
| \( 160 \)-\( 170 \) |
4 |
| \( 170 \)-\( 180 \) |
2 |
| Totale | 20 |
I dati raccolti possono infine essere rappresentati graficamente in modo da rendere più agevole la loro interpretazione, per mezzo di ideogrammi, aerogrammi, istogrammi, etc.
Rappresentiamo i dati dell'esempio precedente in un istogramma:
1.3 Valori medi
In una raccolta dati, l'intervallo compreso tra il valore minimo e il valore massimo costituisce <<la gamma>> delle distribuzioni.
Quando i dati sono stati ordinati in una tabella o in un grafico di frequenza è interessante rilevare i valori medi e precisamente la media, la moda e la mediana.
- La moda è il valore più comune, ovvero quello che compare più frequentemente.
- La media aritmetica è il numero che si ottiene addizionando tutti i dati e dividendo il risultato per il numero totale dei dati.
- La mediana è l'elemento centrale di una raccolta di dati disposti in ordine crescente. Così se i dati sono in numero dispari la mediana è immediatamente individuata, se sono in numero pari è la media aritmetica dei due dati centrali.
Esempio
Utilizziamo i dati dell'esempio precedente (altezze espresse in cm) e ordiniamoli in ordine crescente:
| 140 | 142 | 142 | 144 | 148 | 149 | 150 | 151 | 153 | 153 |
|---|---|---|---|---|---|---|---|---|---|
| 153 | 155 | 156 | 158 | 161 | 165 | 168 | 168 | 170 | 171 |
- La moda è \(53\).
- La media è: \( \dfrac{140+142\cdot 2+144+148+149+150+151+153\cdot 3+155+156+158+161+165+168\cdot 2+170+171}{20} = 154.85\).
- La mediana è \(53\).