4.2 Probabilità
| Sito: | E-Learning PP&S |
| Corso: | Naretti Flavio - Istituti Secondari di Primo Grado - 3E |
| Libro: | 4.2 Probabilità |
| Stampato da: | Utente ospite |
| Data: | venerdì, 2 maggio 2025, 16:46 |
2.1 La probabilità: scienza del caso
Il calcolo della probabilità ci dà notizie sulla possibilità che un dato evento si verifichi oppure no. Attraverso il calcolo delle probabilità è possibile fare delle previsioni per il futuro, così ad esempio gli industriali, gli scienziati, gli uomini di governo, possono in anticipo avere informazioni sulle possibilità che certi avvenimenti si avverino oppure no.
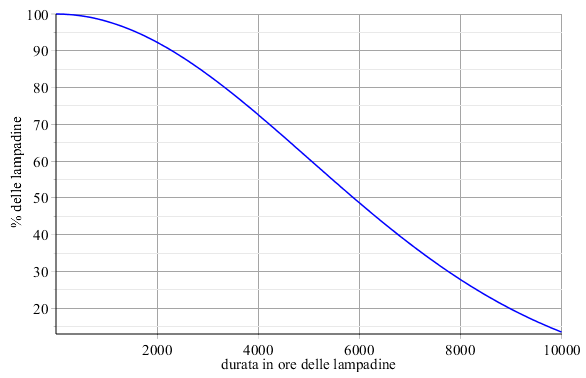
Si abbia ad esempio una fabbrica che produce un certo tipo di lampadine.
In generale, una lampadina fa luce per 2000 ore, ma evidentemente vi saranno nella produzione lampadine che non arrivano a tale durata o altre che la superano. Si ricorre allora, per dare eventuali garanzie agli acquirenti, ad un'indagine statistica su un certo numero di lampadine campione, se ne costruisce il grafico corrispondente e la curva ottenuta è, matematicamente parlando, una funzione che definisce la probabilità che una lampadina duri x ore.
Così, ad esempio, dalla seguente figura risulta che vi è un 28% circa di probabilità che duri 8000 ore e praticamente nessuna probabilità che superi le 10000 ore.
2.2 La probabilità matematica
La probabilità matematica di un evento è data dal rapporto tra il numero dei casi favorevoli a quell'evento e il numero dei casi possibili.
Indicando con \( f\) il numero dei casi favorevoli e \(n\) il numero dei casi possibili, sarà:
\(p=\dfrac{f}{n}\)
Ad esempio, lanciando una moneta si hanno due casi possibili (testa o croce) e di conseguenza il numero dei casi favorevoli (cioè che si presenti una a scelta delle due facce) è \( 1 \). In base alla definizione data di probabilità si avrà dunque che la probabilità matematica che si presenti testa è \(\dfrac{1}{2}\), così come la probabilità matematica che si presenti croce.
Cioè lanciando una moneta c'è un \(50 \%\) di probabilità che esca testa e un un \(50 \%\) di probabilità che esca croce.
Proviamo a lanciare una moneta 20 volte e a segnare il numero delle volte (frequenza) che si presenta testa e il numero delle volte che si presenta croce in una tabella come la seguente:
| Faccia presentata | Annotazioni | Frequenza | Frequenza relativa (frequenza/n° di lanci) |
|---|---|---|---|
| testa | | | | | .../20 | |
| croce | | | .../20 | |
| Totale | 20 |
Noteremo che:
\( \displaystyle frequenza \hspace{0.1 cm} relativa=\frac{frequenza \hspace{0.1 cm} di \hspace{0.1 cm} un \hspace{0.1 cm}evento}{n° \hspace{0.1 cm} di \hspace{0.1 cm} lanci } \simeq \dfrac{1}{2} \)
Infatti il valore della probabilità matematica e il dato sperimentale della frequenza relativa sono valori molto vicini, specialmente se viene effettuato un grande numero di prove (in questo caso lanci di monete), cioè:
\( \displaystyle probabilità \hspace{0.1 cm} matematica \simeq frequenza \hspace{0.1 cm} relativa \)
Questo risultato è noto come legge empirica del caso: quando si realizza un grande numero di prove, la frequenza relativa con cui si verifica un evento è all'incirca uguale alla sua probabilità.