Un polinomio di grado n a coefficienti reali nella sola variabile x, che indichiamo con P(x), può essere scritto ordinatamente, secondo le potenze decrescenti di x:

$P(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + ... + a_1 x + a_0$

con $n \in \mathbb{N}$ e $a_0,...,a_n \in \mathbb{R}$.

Il teorema di Ruffini stabilisce che il valore che il polinomio P(x) assume sostituendo a x il numero $r \in \mathbb{R}$ è uguale al resto della divisione di P(x) per il binomio $A(x) = x - r$.

Il polinomio P(x) è quindi divisibile per il binomio $A(x)$ se e solo se $r$ è uno zero di P(x), cioè se e solo se $P(r) = 0$.

Dividendo P(x) per A(x), si ottiene il polinomio quoziente

$Q(x) = b_{n-1} x^{n-1} + b_{n-2} x^{n-2} +... + b_1 x +b_0$

La divisione polinomiale può essere eseguita con il seguente algoritmo, noto come "regola di Ruffini":

1. i coefficienti di P(x) vengono scritti tra le due linee verticali e il termine noto a destra di esse;
2. si riporta sotto la linea il primo coefficiente;
3. si moltiplica il coefficiente scritto ($a_n$) per $r$ e si scrive il risultato nella colonna successiva, sotto il secondo termine ($a_{n-1}$); 
4. si esegue l'addizione in colonna e si individua così un nuovo coefficiente;
5. si ripete l'operazione per ogni coefficiente.

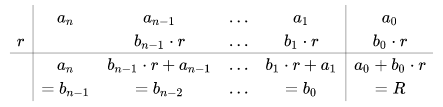
I coefficienti $b_{n-1},...,b_0$ sono i coefficienti del polinomio quoziente Q(x), mentre R è il resto della divisione, che è nullo se r è uno zero del polinomio.