2.2 La distribuzione normale
View
distribuzione normale
1. La distribuzione normale
Se si riportano su di un istogramma le frequenze dei dati statistici raccolti e si collegano i punti medi delle basi superiori dei rettangoli si ottiene una linea spezzata; quest'ultima avrebbe una forma a “campana” se si avesse a disposizione un gran numero di dati. La curva teorica che descrive la campana si chiama gaussiana o curva di Gauss, dal grande matematico Karl Friedrich Gauss (1777-1855).
La distribuzione Gaussiana è la distribuzione di probabilità che meglio rappresenta molte variabili biologiche, ed è anche la distribuzione di probabilità degli errori casuali e delle statistiche campionarie.
La distribuzione gaussiana o “normale” comprende una famiglia di curve, i cui parametri sono la media μ e la deviazione standard σ.
Data una variabile la cui distribuzione di probabilità è gaussiana, possiamo misurare la probabilità corrispondente a determinati intervalli di valori della variabile.
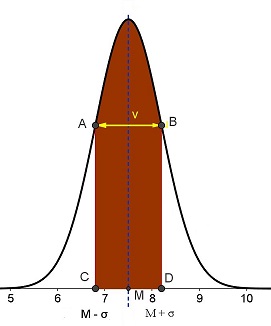
Nel grafico seguente la fascia colorata di marrone sotto la curva gaussiana, che ha per estremi i punti C e D, sta a significare che il 68% dei dati della popolazione indagata si distribuisce tra M–σ e M+σ. I punti C e D hanno rispettivamente ascissa pari a M–σ e M+σ, dove M è la media della distribuzione.
Se invece prendiamo come ascisse dei punti C e D rispettivamente i valori M–2σ e M+2σ, allora la fascia colorata sotto la curva gaussiana che ha per estremi i punti C e D indicherà che il 95 \% dei dati della popolazione indagata si distribuisce tra M–2σ e M+2σ.
In ultimo, se invece prendiamo come ascisse dei punti C e D i valori M–3σ e M+3σ, allora la fascia colorata sotto la curva gaussiana che ha per estremi i punti C e D indicherà che il 99 \% dei dati della popolazione indagata si distribuisce tra M–3σ e M+3σ.
La distribuzione Gaussiana è la distribuzione di probabilità che meglio rappresenta molte variabili biologiche, ed è anche la distribuzione di probabilità degli errori casuali e delle statistiche campionarie.
La distribuzione gaussiana o “normale” comprende una famiglia di curve, i cui parametri sono la media μ e la deviazione standard σ.
- La media determina la posizione centrale della curva. La curva, infatti, risulta simmetrica rispetto al valore medio, μ, della distribuzione dei dati.
- La deviazione standard determina l'ampiezza della curva.
Nel grafico sottostante potete osservare che: - Se la deviazione standard è piccola, la curva è stretta ed allungata. Ciò significa che i dati si addensano attorno al valore medio della distribuzione.
- Se la deviazione standard è grande, la curva si abbassa e si allarga. Ciò significa che i dati si addensano di meno rispetto al valore medio, ovvero i dati si disperdono di più e si allontanano dal valore medio.
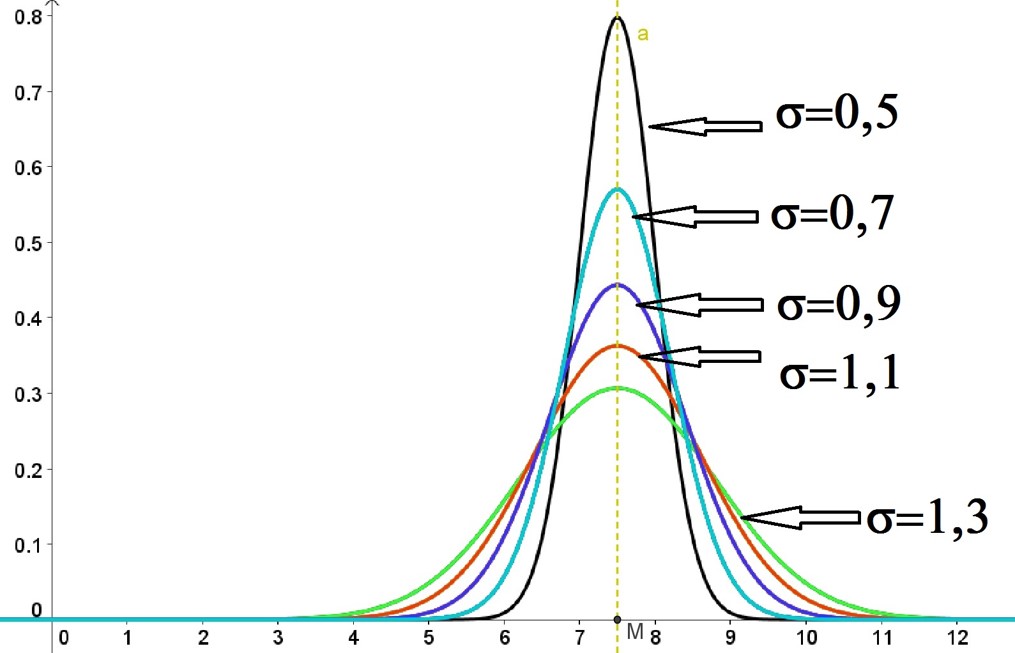
Il grafico riporta diverse gaussiane tutte simmetriche rispetto allo stesso valore medio, M.
Data una variabile la cui distribuzione di probabilità è gaussiana, possiamo misurare la probabilità corrispondente a determinati intervalli di valori della variabile.
Nel grafico seguente la fascia colorata di marrone sotto la curva gaussiana, che ha per estremi i punti C e D, sta a significare che il 68% dei dati della popolazione indagata si distribuisce tra M–σ e M+σ. I punti C e D hanno rispettivamente ascissa pari a M–σ e M+σ, dove M è la media della distribuzione.

Se invece prendiamo come ascisse dei punti C e D rispettivamente i valori M–2σ e M+2σ, allora la fascia colorata sotto la curva gaussiana che ha per estremi i punti C e D indicherà che il 95 \% dei dati della popolazione indagata si distribuisce tra M–2σ e M+2σ.
In ultimo, se invece prendiamo come ascisse dei punti C e D i valori M–3σ e M+3σ, allora la fascia colorata sotto la curva gaussiana che ha per estremi i punti C e D indicherà che il 99 \% dei dati della popolazione indagata si distribuisce tra M–3σ e M+3σ.
