\( \displaystyle \lim_{x \to +\infty}{f(x)}=l \)

se per ogni intorno di \( l \) di raggio \( \epsilon \) esiste un numero reale \( M>0 \) tale che:

\( |x|>M \Rightarrow |f(x)-l|<\epsilon \),

ovvero se \( f(x) \) si avvicina arbitrariamente ad \( l \) a patto di prendere \( x \) sufficientemente grande.

In tale caso la retta \( y=l \) è un asintoto orizzontale per la funzione. 

Esempio. Dato il limite:

\( \displaystyle \lim_{x \to +\infty}{e^{-x}+2}=2 \)

Si può vedere dalla figura:

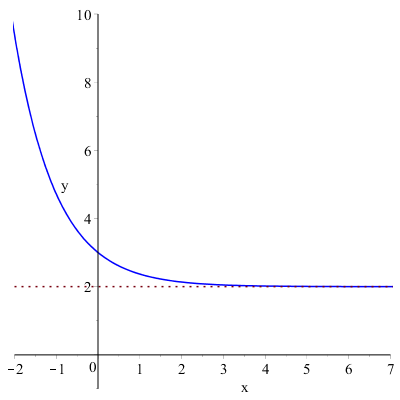
che più i valori della variabile \( x \) aumentano (tendendo a infinito), più i valori della variabile \( y \) si avvicinano al valore \( 2 \), ovvero la funzione si avvicina alla retta \( y=2 \) che rappresenta un asintoto orizzontale.