Calcolo dei limiti
1. Proprietà dei limiti
1.1. Operazioni con limiti infiniti e forme indeterminate
Operazioni con limiti infiniti
- Se esiste il \( \displaystyle \lim_{x \to a}{f(x)}=\infty \), allora esiste il \( \displaystyle \lim_{x \to a}{\dfrac{1}{f(x)}}=0\).
\( f \) infinito \( \Rightarrow \) \( \dfrac{1}{f(x)} \) infinitesimo
- Se \( y=f(x) \) e \( y=g(x) \) tendono entrambe a \( +\infty \) o \( -\infty \), per \( x \) tendente ad \( a \), anche la funzione \( y=f(x)+g(x) \) tende rispettivamente a \( +\infty \) o \( -\infty \).
NOTA BENE: Il teorema non dice nulla nel caso in cui le due funzioni tendano ad infinito ma con segno diverso: in questo caso si ottiene un situazione indeterminata.
Per le operazioni con limiti infiniti si ottengono le seguenti forme indeterminate:
| \( \infty - \infty \) | \( 0 \cdot \infty \) | \( \dfrac{0}{0} \) | \( \dfrac{\infty}{\infty} \) |
|---|
Ottenere una forma indeterminata non significa che il limite non esiste, ma solo che il limite non è determinabile con le regole operative stabilite dai teoremi.
Esempio. Determinare:
\( \displaystyle \lim_{x \to \infty}\dfrac{x^3+2x^2-3}{4x^3-x+1}=\infty \)
Sostituendo il valore \( \infty \) alla variabile \( x \) otteniamo la forma indeterminata \( \dfrac{\infty}{\infty} \).
Allora riscriviamo la funzione ponendo in evidenza \( x^3 \) al numeratore e al denominatore
e semplificando:\( \displaystyle \lim_{x \to \infty}\dfrac{x^3 \left (1+\dfrac{2}{x}-\dfrac{3}{x^3} \right )}{x^3 \left (4-\dfrac{1}{x^2}+\dfrac{1}{x^3} \right )}=\dfrac{1}{4} \)
Infatti quando \( x \) tende ad infinito, i termini che contengono una potenza di \( x \) al denominatore tendono a zero.
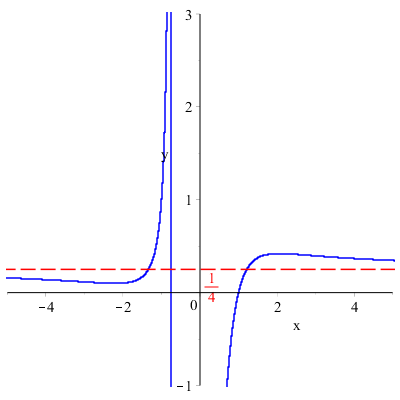
Graficamente questo risultato significa che la funzione ha un asintoto orizzontale di equazione \( y=\dfrac{1}{4} \).