Calcolo dei limiti
View
1. Proprietà dei limiti
1.3. Calcolo dei limiti
Poiché normalmente anche le funzioni più complesse sono il risultato della composizione di funzioni elementari, è indispensabile conoscere bene il valore dei limiti delle funzioni elementari agli estremi del loro dominio:
- funzione identità: \( f(x)=x \)
\( \displaystyle \lim_{x \to -\infty}{f(x)}=-\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione potenza con esponente pari: \( f(x)=x^n \) con \( n \) pari
\( \displaystyle \lim_{x \to -\infty}{f(x)}=+\infty\); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione potenza con esponente dispari: \( f(x)=x^n \) con \( n \) dispari
\( \displaystyle \lim_{x \to -\infty}{f(x)}=-\infty\); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \)
- funzione esponenziale con base maggiore di 1: \( f(x)=a^x \) con \( a>1 \)
\( \displaystyle \lim_{x \to -\infty}{f(x)}=0 \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione esponenziale con base minore di 1: \( f(x)=a^x \) con \(0< a<1 \)
\( \displaystyle \lim_{x \to -\infty}{f(x)}=+\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=0 \) - funzione logaritmica con base maggiore di 1: \( f(x)=\log_a{x} \) con \( a>1 \)
\( \displaystyle \lim_{x \to 0^+}{f(x)}=-\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \) - funzione logaritmica con base minore di 1: \( f(x)=\log_a{x} \) con \( 0<a<1 \)
\( \displaystyle \lim_{x \to 0^+}{f(x)}=+\infty \); \( \displaystyle \lim_{x \to +\infty}{f(x)}=-\infty \)
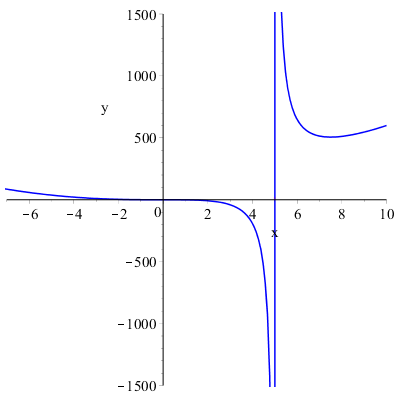
possiamo dedurre che:
\( \displaystyle \lim_{x \to -\infty}{f(x)}=+\infty \)
\( \displaystyle \lim_{x \to +\infty}{f(x)}=+\infty \)
\( \displaystyle \lim_{x \to 5^-}{f(x)}=-\infty \)
\( \displaystyle \lim_{x \to 5^+}{f(x)}=+\infty \)
la retta \(x=5\) è un asintoto verticale.
