2.2 Risolvere un'equazione
View
In questo libro si spiega come risolvere equazioni di primo grado
2.4 Risoluzione grafica di un'equazione
Equazioni determinate, indeterminate, impossibili
Come abbiamo visto prima, ogni equazione di primo grado in un'incognita può essere interpretata graficamente come una coppia di rette; la soluzione dell'equazione corrisponde all'intersezione. In particolare:
Un'equazione determinata ammette una e una sola soluzione, e corrisponde ad una coppia di rette incidenti, che si incontrano in un unico punto.
Ad esempio, l'equazione 2x−5=−3x, che ha soluzione x=1 può essere rappresentata come la coppia di rette
y=2x−5
y=−3x+1
che si intersecano nel punto (1,−3)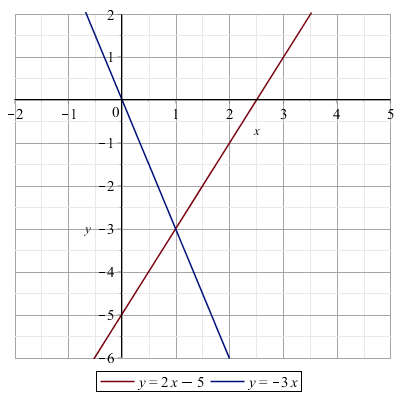
- Un'equazione indeterminata ammette infinite soluzioni (tutti i numeri reali) e corrisponde ad una coppia di rette coincidenti (si incontrano in tutti i loro punti).
Ad esempio, l'equazione 3x−1=3(x+1)−4, la cui soluzione è indeterminata, può essere rappresentata come la coppia di rette
y=3x−1
y=3(x+1)−4
che sono coincidenti.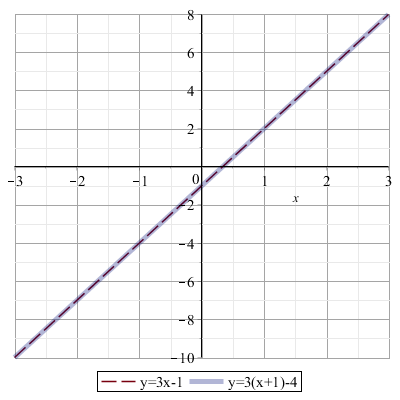
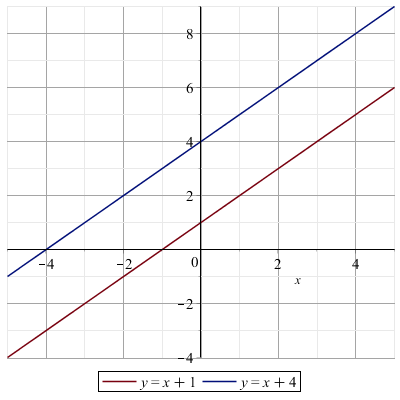
- Un'equazione impossibile corrisponde ad una coppia di rette parallele: non si incontrano mai.
Ad esempio, l'equazione x+1=x+3, che è impossibile, può essere rappresentata come la coppia di rette
y=x+1
y=x+3
che sono parallele.