1.1 Definizione di limite
1. Definizione di limite
1.1. Definizione limite finito al finito
Definizione. Si dice che \( l \in \mathbb{R} \) è il limite della funzione \( y=f(x) \) per \( x \) che tende ad \( a \in \mathbb{R} \) e si scrive
\( \displaystyle \lim_{x \to a}{f(x)}=l \)
se per ogni \( \epsilon >0 \) esiste un numero \( \delta >0 \) tale che:
\( \forall x (|x-a| <\delta, x \neq a) \Rightarrow |f(x)-l|<\epsilon \),
ovvero se \( f(x) \) si avvicina arbitrariamente ad \( l \) a patto di prendere \( x \) sufficientemente vicino a \( a \).
Esempio. Dato il seguente limite:
\( \displaystyle \lim_{x \to 4}{\dfrac{3x}{x-2}}=6 \)
Scegliamo sull'asse delle \( y \) un intorno di \( 6 \), ovvero un intervallo aperto di piccole dimensioni \( \left ]6-\epsilon,6+\epsilon \right[ \) e notiamo come questo intorno ne individua uno corrispondente di \( 4 \) sull'asse \( x \).
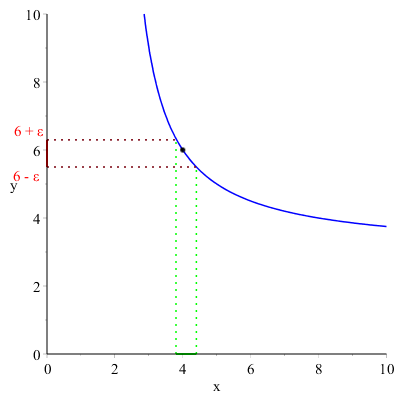
Facendo variare \( \epsilon \), piccolo a piacere e positivo, e di conseguenza l'intorno sull'asse \( y \), i punti della funzione che sono compresi fra le due rette orizzontali hanno le loro ascisse nell'intorno di \( 6 \).
NOTA BENE: La condizione \( x \neq a \) presente nella definizione, sta a significare che nel caso in cui la funzione non esistesse nel punto di ascissa \( a \) o avesse in esso un punto isolato la definizione di limite funziona ugualmente. Quindi il risultato del limite non dà alcuna informazione sul comportamento della funzione nel punto.
