Calcolo dei limiti
1. Proprietà dei limiti
1.2. Infinitesimi e infiniti
Può capitare di dover calcolare un limite che presenta la forma indeterminata \( \dfrac{0}{0} \), senza che sia possibile semplificare la funzione fratta. Si può allora giungere ad un risultato confrontando gli infinitesimi, cioè controllando quale fra la funzione che sta al numeratore e la funzione che sta al denominatore tende a zero più rapidamente.
Per questo scopo può aiutare il confronto fra grafici:
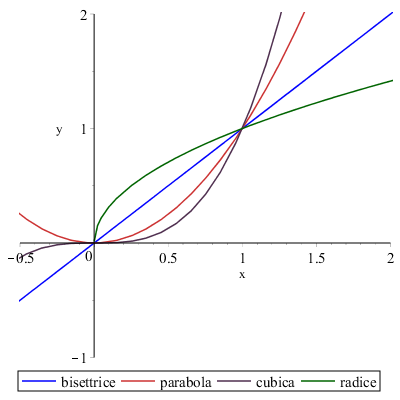
Se consideriamo il comportamento nell'intorno di zero delle funzioni disegnate vediamo che l'ordine con cui si avvicinano più velocemente allo zero è:
- cubica
- parabola
- bisettrice
- radice
Ciò significa che dalla cubica alla radice l'ordine di infinitesimo decresce. Di seguito alcuni esempi di limiti, che coinvolgono queste funzioni, la cui forma indeterminata è \( \dfrac{0}{0} \):
\( \displaystyle \lim_{x \to 0^+}{\dfrac{\sqrt{x}}{x^2}}=\infty \); \( \displaystyle \lim_{x \to 0^+}{\dfrac{x^3}{\sqrt{x}}}=0 \); \( \displaystyle \lim_{x \to 0^+}{\dfrac{x^3}{x^2}}=0 \)
Allo stesso modo può capitare di dover calcolare un limite che presenta la forma indeterminata \( \dfrac{\infty}{\infty} \), senza che sia possibile semplificare la funzione fratta. Si può allora giungere ad un risultato confrontando gli infiniti, cioè controllando quale fra la funzione che sta al numeratore e la funzione che sta al denominatore tende a infinito più rapidamente.
Per questo scopo può aiutare il confronto fra grafici:
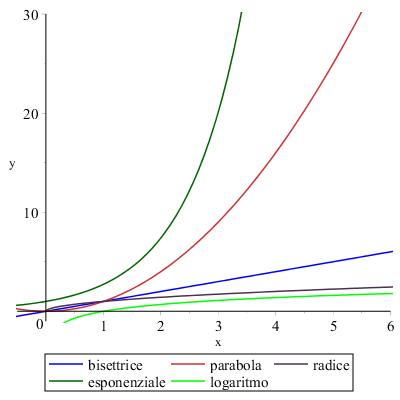
Se consideriamo il comportamento nell'intorno di \( +\infty \) delle funzioni disegnate vediamo che l'ordine con cui si avvicinano più velocemente a \( +\infty \) è:
- esponenziale
- parabola
- bisettrice
- radice
- logaritmo
Ciò significa che dall'esponenziale al logaritmo l'ordine di infinito decresce. Di seguito alcuni esempi di limiti, che coinvolgono queste funzioni, la cui forma indeterminata è \( \dfrac{\infty}{\infty} \):
\( \displaystyle \lim_{x \to +\infty}{\dfrac{e^x}{\sqrt{x}}}=\infty \); \( \displaystyle \lim_{x \to +\infty}{\dfrac{\ln{x}}{x}}=0 \); \( \displaystyle \lim_{x \to +\infty}{\dfrac{x^2}{\ln{x}}}=\infty \);
