Continuità di una funzione
Visualizzare
1. Le funzioni continue
1.1. Punti di discontinuità
I casi di discontinuità di una funzione possono essere di diverso tipo:
- discontinuità di prima specie: se i suoi limiti sinistro e destro per x che tende a \(a\) esistono finiti ma sono diversi tra loro. Almeno uno dei due limiti risulta diverso da \( f(a) \) e si chiama salto della funzione in \( a \) il valore assoluto della differenza dei due limiti.
Esempio: La funzione \( f(x)= \begin{cases} 1 \quad x \geq 0\\ -1 \quad x<0 \end{cases} \)
presenta una discontinuità di prima specie nel punto \( x=0 \) poiché: \( \displaystyle \lim_{x \to 0^-} f(x)=-1 \) e \( \displaystyle \lim_{x \to 0^+} f(x)=1 \). Il salto è pari a 2.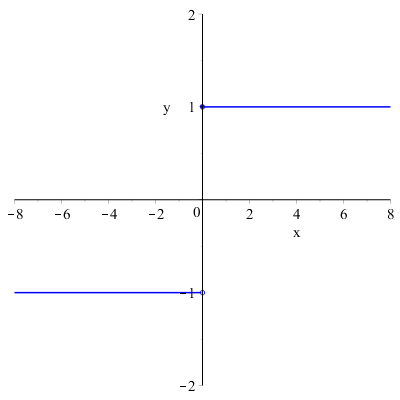
discontinuità di seconda specie: se per x che tende ad \(a\) almeno uno dei suoi limiti sinistro e destro o non esiste o vale \( \pm \infty \).
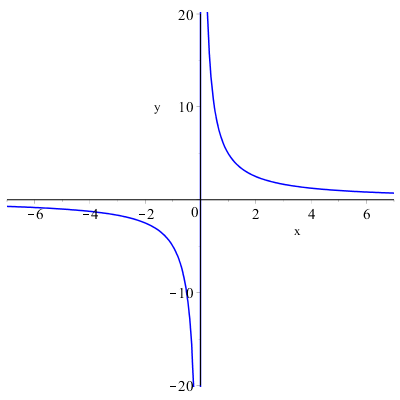
Esempio: La funzione \( y=\dfrac{1}{x} \) presenta nel punto \( x=0 \) una discontinuità di seconda specie essendo:
\( \displaystyle \lim_{x \to 0^-} f(x)=-\infty \) e \( \displaystyle \lim_{x \to 0^+} f(x)=+\infty \).
- discontinuità di terza specie o eliminabile: se esiste finito il limite per x che tende a \(a\) (cioè i suoi limiti sinistro e destro esistono e sono uguali tra loro), ma tale limite non coincide con il valore della funzione in \(a\). Il termine eliminabile sta ad indicare che la funzione può essere facilmente resa continua in \(a\) modificando il suo valore in \(a\) e ponendo \( l=f(a) \) nel caso in cui \( a \) non sia nel dominio, oppure inserendo il punto \(a\) nel dominio.
Esempio: La funzione \( f(x)=\begin{cases} \ln{x} \quad x \neq 1\\ 2 \quad x=1 \end{cases} \)
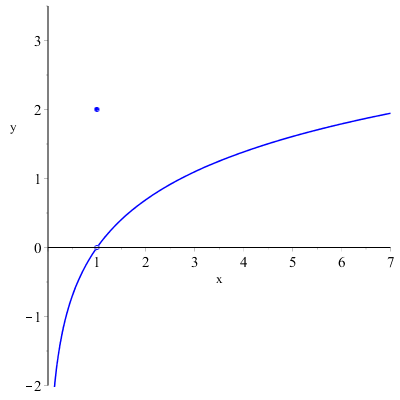
presenta nel punto \( x=1 \) una discontinuità di terza specie essendo: \( \displaystyle \lim_{x \to 1} f(x)=0 \), ma \( f(1)=2 \).
