Dato che le successioni sono definite da funzioni, è possibile calcolarne il limite per studiarne l'andamento al crescere di $n$, ovvero $\displaystyle \lim_{n \to +\infty} a_n$.

Una successione può essere

• convergente: se esiste finito il $\displaystyle \lim_{n \to +\infty} a_n$.
  Ad esempio, $a_n=2-\dfr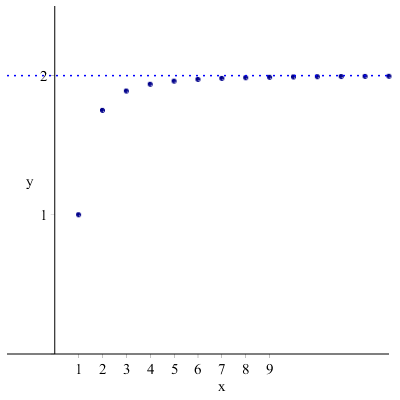ac{1}{n^2}$
  

  

• divergente: se esiste infinito il $\displaystyle \lim_{n \to +\infty} a_n$.
  Ad esempio, $a_n=3n^3$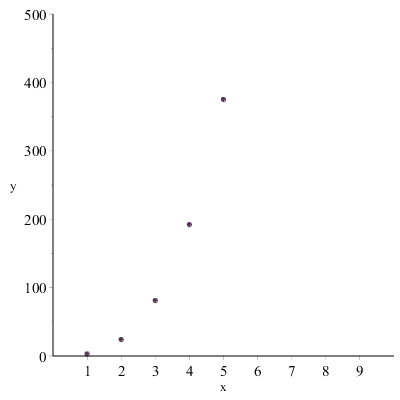
  
  
• irregolare: se il limite non esiste.
  Ad esempio, $a_n=\sin{\dfr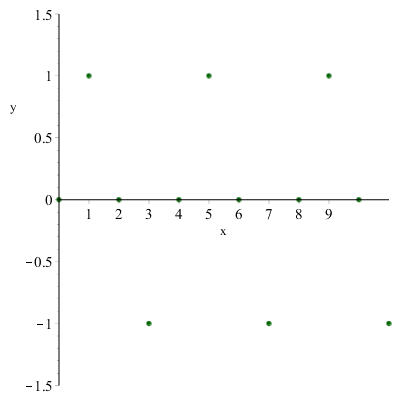ac{n\pi}{2}}$
  
  

Non bisogna confondere la caratteristica di una successione di essere convergente o divergente con quella di essere crescente o decrescente. Quest'ultime indicano solo che i termini sono via via rispettivamente più grandi (per ogni $n$, $a_n>a_{n-1}$) o più piccoli (per ogni $n$, $a_n<a_{n-1}$), e indicano la possibilità che la successione sia limitata.

NOTA BENE. Una successione può essere crescente senza essere divergente, e una successione decrescente può essere divergente.

Esempio: Determiniamo il carattere della successione $a_n=1 + \frac{1}{3n}$ attraverso il calcolo del limite:

$\displaystyle \lim_{n \to +\infty} \left( 1 + \frac{1}{3n} \right)^{2n}=\Bigr[ \displaystyle \lim_{n \to +\infty} \left( 1 + \frac{1}{3n} \right)^{3n} \Bigl]^{\frac{2}{3}}=e^{\frac{2}{3}}=\sqrt[3]{e^2}$

si tratta di una successione regolare convergente.

Esempio: Determiniamo il carattere della successione $\dfrac{n^{6} + \ln{n} + 3^{n}}{2^{n} + n^{4} + \ln^{5}{n}}$:

$\displaystyle \lim_{n \to +\infty} \frac{n^{6} + \ln{n} + 3^{n}}{2^{n} + n^{4} + \ln^{5}{n}}=\displaystyle \lim_{n \to +\infty} \frac{3^{n}}{2^{n}}=+ \infty$

Si tratta di una successione regolare divergente.