Le successioni
1. Le successioni numeriche
I numeri naturali, i numeri pari e dispari, i numeri primi sono esempi di successioni numeriche. Sono insiemi numerici infiniti, numerabili, linearmente ordinati e discreti (è possibile fornire un elenco dei loro elementi, indicando qual è il primo di essi e come si ottiene da un elemento il suo successivo). Ogni elemento o termine della successione è individuato dal posto che occupa nell'ordinamento: \(a_0, a_1, a_2, ..., a_n, ...\).
Una successione è individuata dalla corrispondenza biunivoca, indicata con \( f \), che associa ad ogni elemento di \( \mathbb{N} \) il corrispondente elemento della successione. Per indicare una successione è sufficiente esprimere il suo termine generico \(a_n \).
Esempio. Qual è la successione individuata dalla funzione \( f(n)=2^{-n}\)?
Costruiamo i primi termini della successione:
\(0 \rightarrow 2^0=1\)
\(1 \rightarrow 2^{-1}=\dfrac{1}{2}\)
\(2 \rightarrow 2^{-2}=\dfrac{1}{4}\)
I termini della successione sono:
\(1, \dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \dfrac{1}{16}, ..., \dfrac{1}{2^n} \)
Se rappresentatiamo graficamente la successione otteniamo:
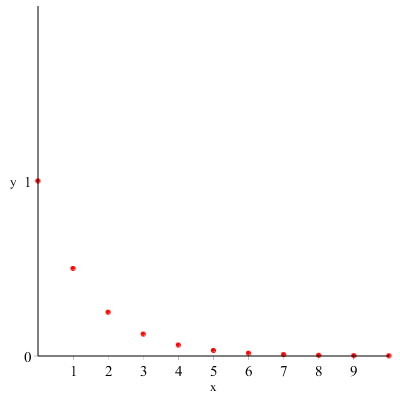
Si può definire una successione:
- per definizione del termine generale, dando la legge che associa al numero naturale n il corrispondente elemento \( a_n \) (come nell'esempio precedente)
- per ricorrenza, ovvero quando il termine generale è espresso in funzione di uno o più termini precedenti; in tal caso la successione può essere calcolata solo quando sono noti i termini iniziali. Ad esempio, la successione definita dalla relazione:
\( a_{n+1}=a_n^2+1 \) con \( a_0=1 \)
esprime la successione i cui primi elementi sono: \( 1, 2, 5, 26, ... \).
Infatti:
\( a_{2}=a_1^2+1=1+1=2 \)
\( a_{3}=a_2^2+1=4+1=5 \)
\( a_{4}=a_3^2+1=25+1=26 \)..
